在导航中,姿态是指车辆或物体相对于固定参考系的朝向,该参考系通常由三个旋转轴定义:纵倾、横滚和偏航。
这些轴描述了车辆在三维空间中的角位置和运动。纵倾是指车辆机头上或下倾斜,横滚表示车辆沿其纵轴的左右倾斜,而偏航表示绕其垂直轴的左右旋转。这些参数共同定义了车辆在其环境中的定位和操纵方式。
姿态对于维持稳定性、确保精确控制以及在各个领域实现精确导航至关重要。例如,在航空中,姿态有助于飞行员或自动驾驶系统保持水平飞行、执行转弯以及调整以应对湍流。
同样,在海上导航中,姿态控制可确保船舶保持直立并保持航向,尽管面临波浪和水流的挑战。
在航天器中,姿态在将天线、太阳能电池板或科学仪器指向正确的方向方面起着至关重要的作用,尤其是在无法获得外部视觉线索时。
为了测量和控制姿态,采用了陀螺仪、加速度计和磁力计等系统,通常集成到惯性导航系统 (INS)中。这些系统与 GNSS 或星跟踪器等外部数据源协同工作,以保持精确的姿态。
在动态环境中,理解和管理姿态尤为重要,在这些环境中,风、波浪或重力异常等外力会影响车辆的轨迹。
因此,有效的姿态控制可确保安全高效的行驶,使车辆能够精确地实现其导航目标。
GNSS 姿态解算
GNSS 姿态解算提供横滚角、俯仰角和偏航角,这些角度描述了物体在空间中的方向。这三个分量对于理解物体相对于地球表面或参考坐标系的姿态至关重要。
- 横滚是指绕前方轴的旋转,影响物体的左右倾斜。
- 俯仰是绕横向轴的旋转,决定了上下倾斜。
- 舶偏是绕垂直轴的旋转,它定义了对象所面向的方向。
这些解决方案结合了来自 GNSS 接收机的数据以及额外的传感器(如加速度计和陀螺仪),以提供高度准确和可靠的姿态信息。
这种方法在需要精确定向的环境中尤其有价值,例如飞机、船舶和自动驾驶车辆的导航系统。通过集成这些不同的传感器输入,系统即使在具有挑战性的条件下也能确保最佳性能。
姿态表示
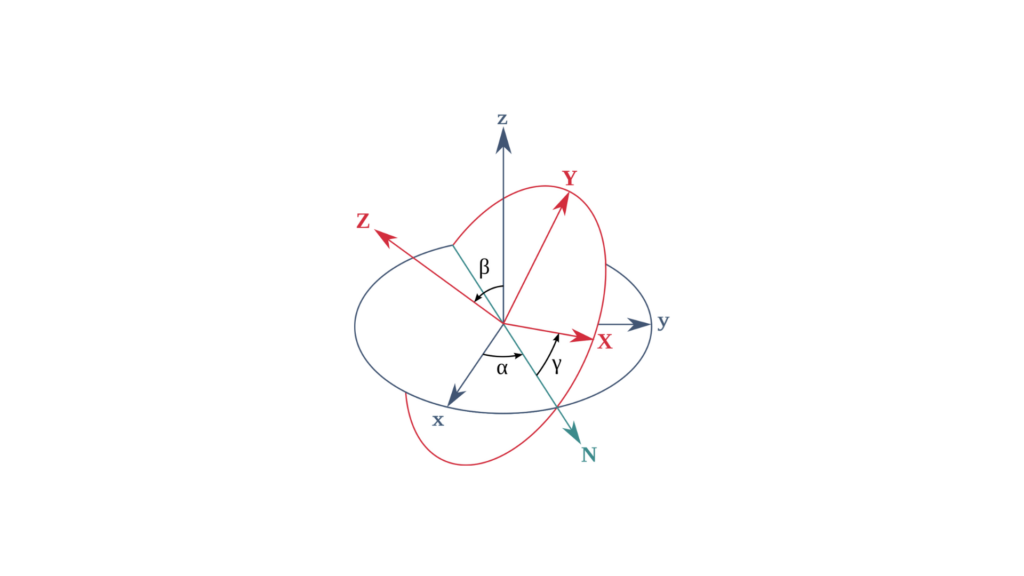
姿态表示物体相对于参考系(例如地球表面)的方向或旋转。在导航系统中,这个概念对于确定物体在空间中的方向至关重要,这可以应用于飞机、无人机、船舶或其他自主系统。有几种方法可以用数学和视觉方式表示姿态。
1 – 欧拉角(横滚、俯仰、偏航)
欧拉角通过三次旋转(横滚、俯仰和偏航)表示物体的姿态。这些角度描述了围绕三个轴按特定顺序进行的旋转,例如:
横滚 (φ):绕前后轴旋转。
俯仰 (θ):绕侧轴旋转。
偏航 (ψ):绕垂直轴旋转。
数学表示
欧拉角可以表示为 3×3 旋转矩阵,其中:
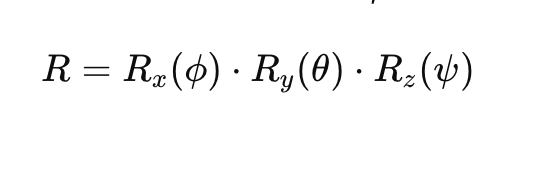
位置:
- Rx(ϕ)R_x(\phi)Rx(ϕ) 是横滚旋转矩阵。
- Ry(θ)R_y(\theta)Ry(θ)是俯仰旋转矩阵。
- Rz(ψ)R_z(\psi)Rz(ψ) 是偏航旋转矩阵。
每个旋转矩阵给出为:
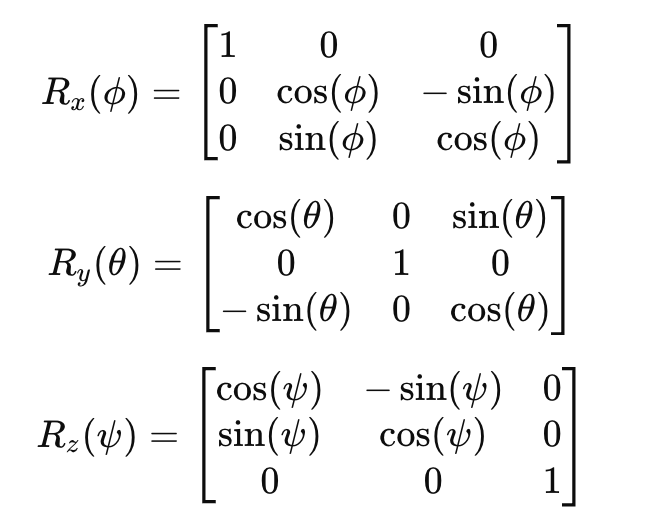
2 – 旋转矩阵
旋转矩阵是表示姿态的另一种方法。在这种方法中,一个 3×3 矩阵描述了物体在 3D 空间中相对于固定坐标系的方向。这些矩阵是正交的,意味着它们的行和列是单位向量。因此,矩阵的逆矩阵就是它的转置。
数学表示
您可以将一个通用的旋转矩阵 𝑅 写成:
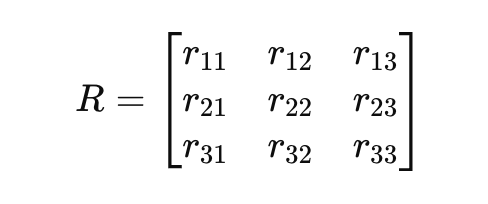
3 – 四元数
四元数提供了一种更紧凑且数值上更稳定的旋转表示方法。它们避免了与欧拉角相关的奇点和万向节锁问题。一个四维向量 𝑞 定义如下:
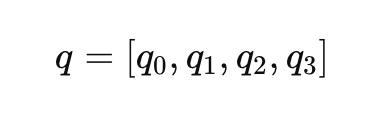
其中 𝑞0 是标量部分,[𝑞1, 𝑞2, 𝑞3] 是向量分量。旋转的四元数表示可以写成:
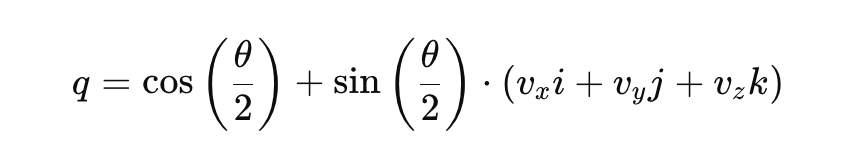
位置:
- θ 是旋转角度。
- [vx,vy,vz] 是表示旋转轴的单位向量。
- i, j, k 是基本四元数单位。
四元数的优势:
- 避免万向节锁和奇点。
- 插值计算效率更高。
4 – 方向余弦矩阵 (DCM)
方向余弦矩阵类似于旋转矩阵,也描述了对象的方向。 DCM 将一个坐标系中向量的坐标与同一向量在另一个坐标系中的坐标相关联。
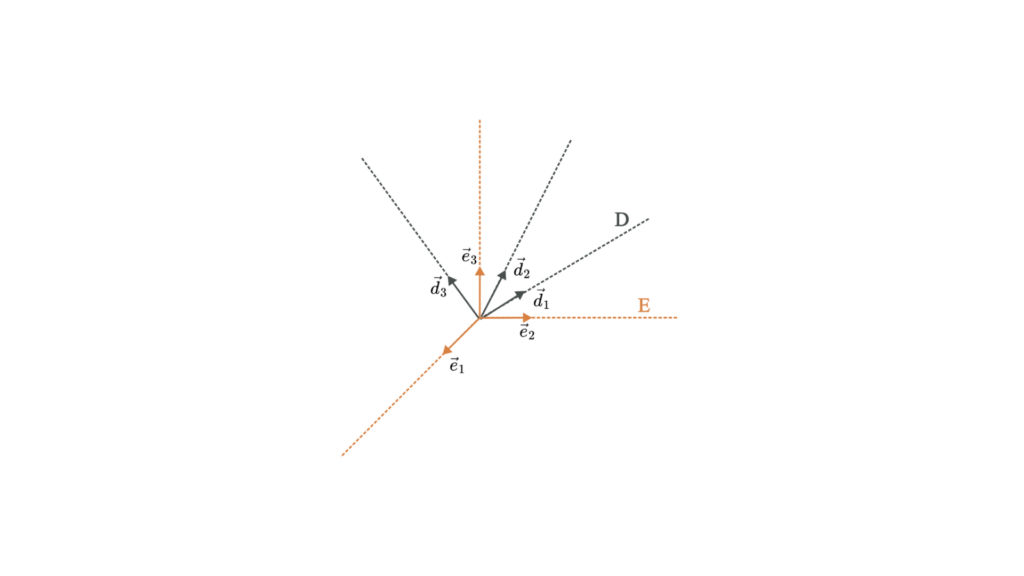
数学表示
方向余弦矩阵 𝐶 是一个 3×3 矩阵,用于定义两个坐标系之间的关系:
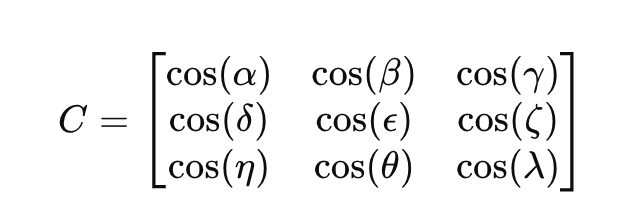
其中元素 cos (⋅) 表示两个坐标系向量之间的角度的余弦值。
请告诉我们您的项目