ナビゲーションにおいて、姿勢とは、固定された参照フレームに対する車両や物体の向きのことで、通常、ピッチ、ロール、ヨーの3つの回転軸によって定義されます。
これらの軸は、3次元空間における車両の角度位置と動きを表します。ピッチは、車両のノーズの上下方向の傾きを指し、ロールは、長軸に沿った車両の左右方向の傾きを表し、ヨーは、垂直軸を中心とした左右方向の回転を表します。これらのパラメータを組み合わせることで、車両が環境内でどのように位置し、操縦されるかが定義されます。
姿勢は、安定性を維持し、正確な制御を確保し、さまざまな領域で正確なナビゲーションを可能にするために不可欠です。たとえば、航空では、姿勢は、パイロットまたは自動操縦システムが水平飛行を維持し、旋回を実行し、乱気流に対応するのに役立ちます。
同様に、海上ナビゲーションでは、姿勢制御により、船舶が波や海流によってもたらされる課題にもかかわらず、直立状態を維持し、コースを維持することができます。
宇宙船では、姿勢は、特に外部からの視覚的な手がかりがない場合に、アンテナ、ソーラーパネル、または科学機器を正しい方向に向ける上で重要な役割を果たします。
姿勢を測定および制御するために、ジャイロスコープ、加速度計、磁力計などのシステムが採用され、多くの場合、慣性航法システム(INS)に統合されています。これらのシステムは、GNSSやスタートラッカーなどの外部データソースと連携して、正確な姿勢を維持します。
姿勢の理解と管理は、風、波、重力異常などの外力が車両の軌道に影響を与える可能性のある動的な環境において特に重要です。
したがって、効果的な姿勢制御は、安全で効率的な移動を保証し、車両が正確にナビゲーションの目的を達成できるようにします。
GNSS姿勢ソリューション
GNSS姿勢ソリューションは、空間内の物体の向きを表すロール、ピッチ、ヨーの角度を提供します。これらの3つのコンポーネントは、地球の表面または参照フレームに対する物体の姿勢を理解するために不可欠です。
- ロールとは、前方軸を中心とした回転のことで、物体の左右の傾きに影響します。
- ピッチとは、左右の軸を中心とした回転で、上下の傾きを決定します。
- ヨー(Yaw)とは、垂直軸を中心とした回転のことで、対象物が向いている方向を定義します。
これらのソリューションは、GNSS受信機からのデータと、加速度計やジャイロスコープなどの追加センサーからのデータを組み合わせて、非常に正確で信頼性の高い姿勢情報を提供します。
このアプローチは、航空機、船舶、自律走行車のナビゲーションシステムなど、正確なオリエンテーションが重要な環境で特に役立ちます。これらの多様なセンサー入力を統合することにより、システムは困難な条件下でも最適なパフォーマンスを保証します。
姿勢の表現
姿勢は、地球の表面などの基準座標系に対する物体の向きまたは回転を表します。ナビゲーション・システムでは、この概念は、航空機、UAV、船舶、またはその他の自律システムに適用できる、空間における物体の向きを決定するために重要です。姿勢を数学的および視覚的に表現する方法はいくつかあります。
1 – オイラー角(ロール、ピッチ、ヨー)
オイラー角は、ロール、ピッチ、ヨーの3つの回転によってオブジェクトの向きを表します。これらの角度は、次のような特定のシーケンスで3つの軸を中心とした回転を表します。
ロール(φ): 前後軸を中心とした回転。
ピッチ(θ): 左右軸を中心とした回転。
ヨー(ψ): 垂直軸を中心とした回転。
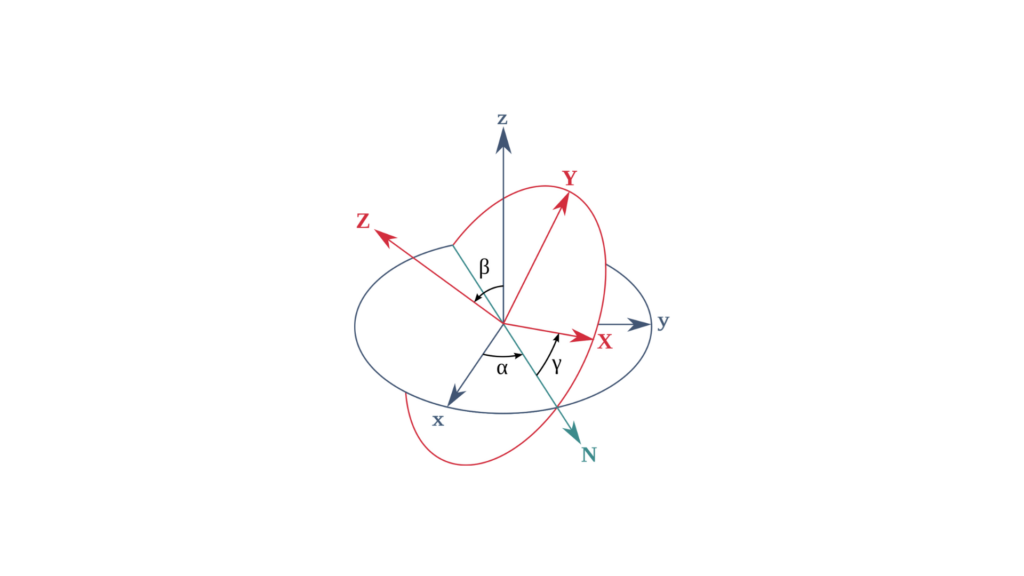
数理表現
オイラー角は、3×3の回転行列として表すことができます。
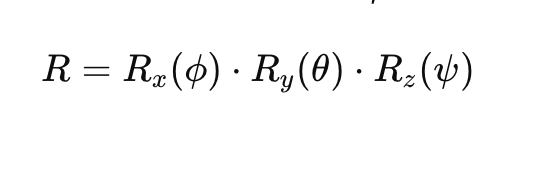
場所:
- Rx(ϕ)R_x(\phi)Rx(ϕ)は、ロールの回転行列です。
- Ry(θ)R_y(\theta)Ry(θ)は、ピッチの回転行列です。
- Rz(ψ)R_z(\psi)Rz(ψ)は、ヨーの回転行列です。
各回転行列は次のように与えられます。
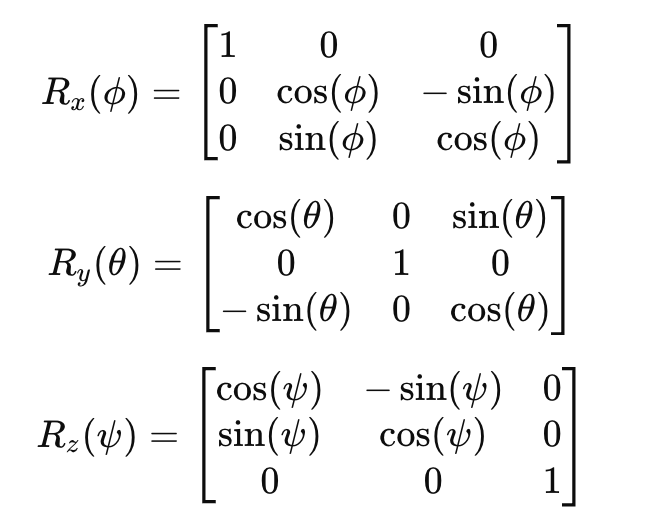
2 – 回転行列
回転行列は、姿勢を表現する別の方法を提供します。この方法では、3×3の行列が、固定座標系に対する3D空間内のオブジェクトの向きを表します。これらの行列は直交行列であり、行と列は単位ベクトルです。したがって、行列の逆行列は単なる転置です。
数理表現
一般的な回転行列𝑅は、次のように記述できます。
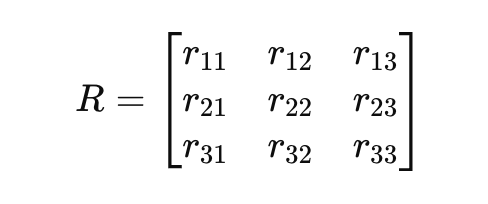
3 – クォータニオン
クォータニオンは、回転をよりコンパクトかつ数値的に安定した表現で提供します。オイラー角に関連する特異点やジンバルロックの問題を回避します。クォータニオン𝑞は4次元ベクトルです:
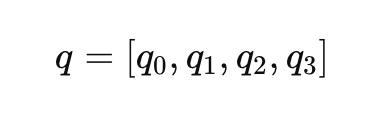
ここで、𝑞0はスカラー部分、[𝑞1, 𝑞2, 𝑞3]はベクトル成分です。回転のクォータニオン表現は、次のように記述できます。
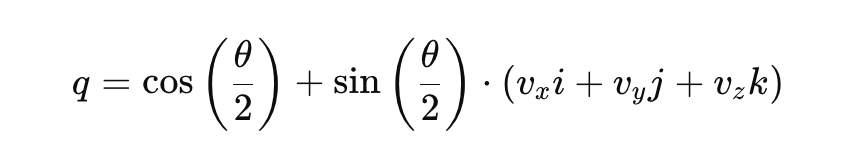
場所:
- θ は回転角です。
- [vx,vy,vz] は、回転軸を表す単位ベクトルです。
- i, j, k は、基本的なクォータニオン単位です。
クォータニオンの利点:
- ジンバルロックや特異点を回避します。
- 内挿の計算効率が向上。
4 – 方向余弦行列(DCM)
方向余弦行列は回転行列に似ており、オブジェクトの向きも記述します。DCMは、あるフレーム内のベクトルの座標を別のフレーム内の同じベクトルの座標に関連付けます。
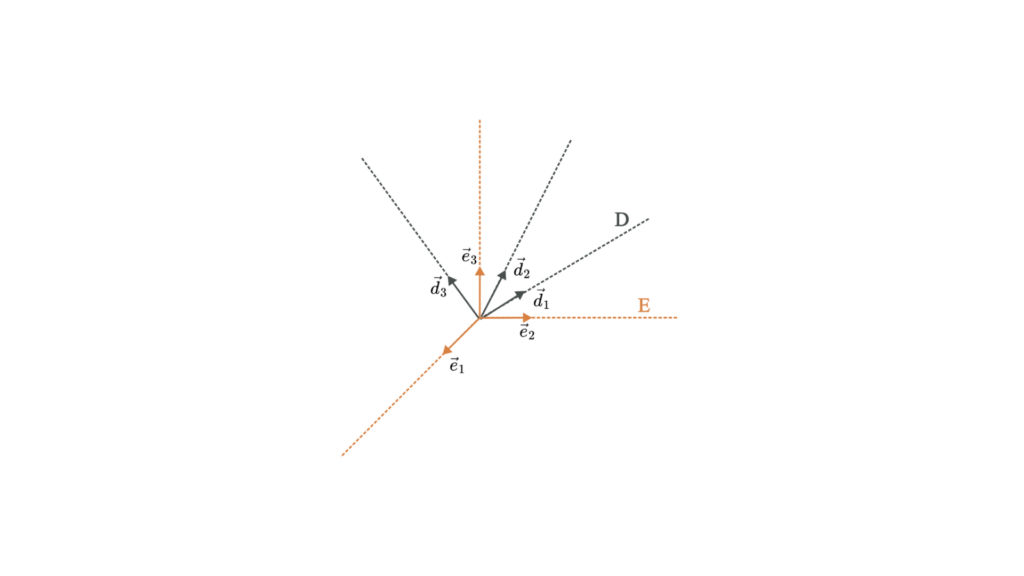
数理表現
方向余弦行列𝐶は、2つの座標フレーム間の関係を定義する3×3行列です。
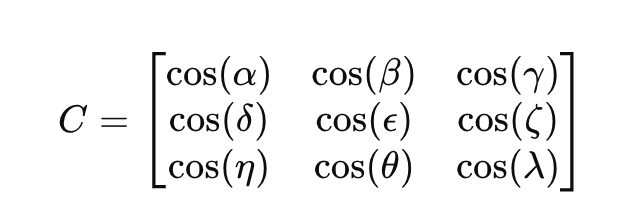
ここで、要素cos(⋅)は、2つの座標フレームのベクトル間の角度のコサインを表します。
お客様のプロジェクトについてお聞かせください