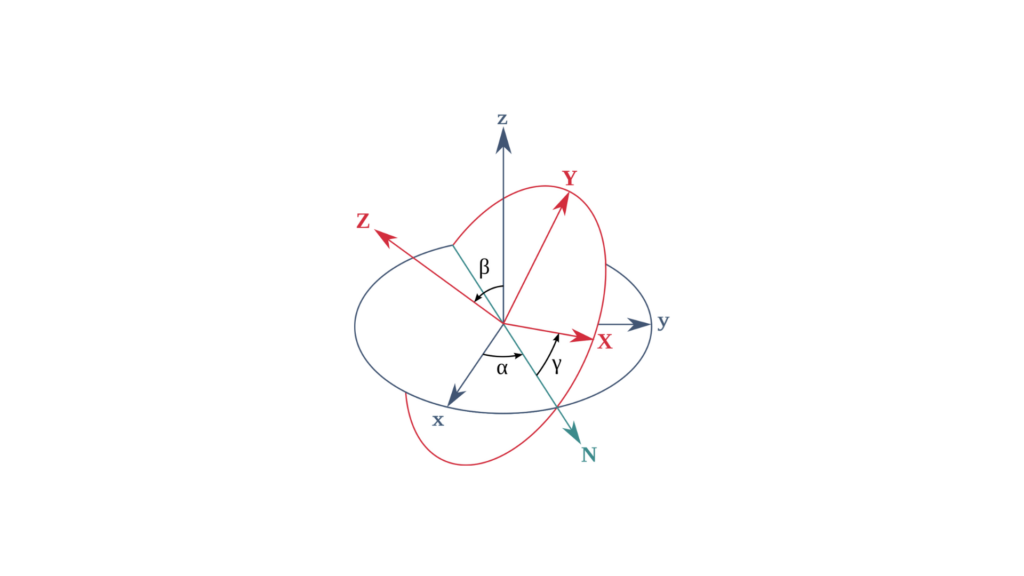
항법에서 자세는 일반적으로 피치, 롤, 요의 세 회전축으로 정의되는 고정된 기준틀을 기준으로 차량 또는 물체의 방향을 나타냅니다.
이러한 축은 3차원 공간에서 차량의 각도 위치와 움직임을 설명합니다. 피치는 차량의 기수가 위 또는 아래로 기울어지는 것을 나타내고, 롤은 세로축을 따라 차량이 좌우로 기울어지는 것을 나타내며, 요는 수직축을 중심으로 좌우 회전을 나타냅니다. 이러한 파라미터들은 함께 차량이 환경에서 어떻게 위치하고 조작되는지를 정의합니다.
자세는 안정성을 유지하고, 정밀한 제어를 보장하며, 다양한 영역에서 정확한 항법을 가능하게 하는 데 매우 중요합니다. 예를 들어 항공에서 자세는 조종사 또는 자동 조종 시스템이 수평 비행을 유지하고, 회전을 실행하고, 난기류에 대비하는 데 도움이 됩니다.
마찬가지로 해상 항법에서 자세 제어는 파도와 해류로 인한 어려움에도 불구하고 선박이 똑바로 코스를 유지하도록 보장합니다.
우주선에서 자세는 특히 외부 시각적 단서를 사용할 수 없을 때 안테나, 태양 전지판 또는 과학 장비를 올바른 방향으로 향하게 하는 데 중요한 역할을 합니다.
자세를 측정하고 제어하기 위해 자이로스코프, 가속도계 및 자력계와 같은 시스템이 사용되며, 종종 관성 항법 시스템(INS)에 통합됩니다. 이러한 시스템은 GNSS 또는 별 추적기와 같은 외부 데이터 소스와 함께 작동하여 정확한 방향을 유지합니다.
자세를 이해하고 관리하는 것은 바람, 파도 또는 중력 이상과 같은 외부 힘이 차량의 궤적에 영향을 미칠 수 있는 동적 환경에서 특히 중요합니다.
따라서 효과적인 자세 제어는 안전하고 효율적인 이동을 보장하여 차량이 정밀하게 항법 목표를 달성할 수 있도록 합니다.
GNSS 자세 솔루션
GNSS 자세 솔루션은 공간에서 물체의 방향을 설명하는 롤, 피치 및 요 각도를 제공합니다. 이러한 세 가지 구성 요소는 지구 표면 또는 기준 프레임을 기준으로 물체의 자세를 이해하는 데 필수적입니다.
- 롤은 전진 축을 중심으로 회전하는 것으로, 물체의 좌우 기울기에 영향을 줍니다.
- 피치는 좌우 축을 중심으로 회전하며, 상하 기울기를 결정합니다.
- Yaw는 수직축을 중심으로 회전하며, 객체가 향하는 방향을 정의합니다.
이러한 솔루션은 GNSS 수신기의 데이터와 가속도계 및 자이로스코프와 같은 추가 센서를 결합하여 매우 정확하고 신뢰할 수 있는 자세 정보를 제공합니다.
이러한 접근 방식은 항공기, 선박 및 자율 차량용 내비게이션 시스템과 같이 정확한 방향이 중요한 환경에서 특히 유용합니다. 이러한 다양한 센서 입력을 통합함으로써 시스템은 까다로운 조건에서도 최적의 성능을 보장합니다.
자세 표현
자세는 지구 표면과 같은 기준 프레임을 기준으로 물체의 방향 또는 회전을 나타냅니다. 내비게이션 시스템에서 이 개념은 항공기, UAV, 선박 또는 기타 자율 시스템에 적용될 수 있는 공간에서 물체의 방향을 결정하는 데 매우 중요합니다. 자세를 수학적 및 시각적으로 표현하는 방법에는 여러 가지가 있습니다.
1 – 오일러 각도(Roll, Pitch, Yaw)
오일러 각도는 롤, 피치, 요 세 번의 회전을 통해 객체의 방향을 나타냅니다. 이러한 각도는 다음과 같이 특정 순서로 세 축을 중심으로 회전을 설명합니다.
Roll (φ): 앞-뒤 축을 중심으로 회전합니다.
Pitch (θ): 좌우 축을 중심으로 회전합니다.
Yaw (ψ): 수직 축을 중심으로 회전합니다.
수학적 표현
오일러 각도는 다음과 같은 3×3 회전 행렬로 표현할 수 있습니다.
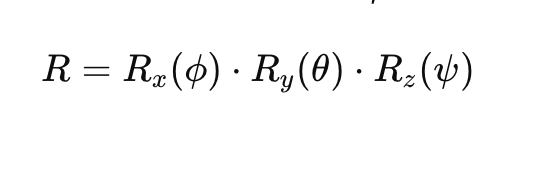
위치:
- Rx(ϕ)R_x(\phi)Rx(ϕ)는 롤에 대한 회전 행렬입니다.
- Ry(θ)R_y(\theta)Ry(θ)는 피치에 대한 회전 행렬입니다.
- Rz(ψ)R_z(\psi)Rz(ψ)는 요에 대한 회전 행렬입니다.
각 회전 행렬은 다음과 같이 주어집니다.
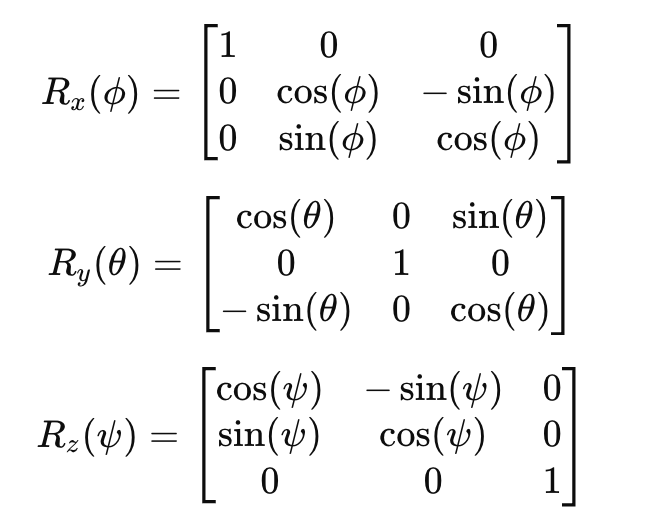
2 – 회전 행렬
회전 행렬은 자세를 나타내는 또 다른 방법을 제공합니다. 이 방법에서 3×3 행렬은 고정된 좌표계를 기준으로 3차원 공간에서 객체의 방향을 설명합니다. 이러한 행렬은 직교하며, 이는 행과 열이 단위 벡터임을 의미합니다. 결과적으로 행렬의 역행렬은 단순히 전치 행렬입니다.
수학적 표현
일반 회전 행렬 𝑅는 다음과 같이 쓸 수 있습니다.
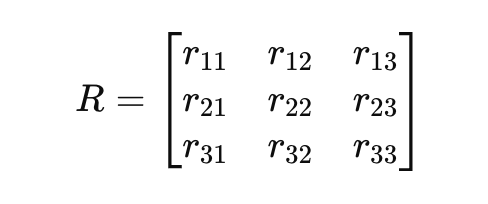
3 – Quaternions
쿼터니언은 회전을 더 간결하고 수치적으로 안정적으로 표현합니다. Euler 각도와 관련된 특이점 및 짐벌 잠금 문제를 피할 수 있습니다. 쿼터니언 𝑞는 4차원 벡터입니다.
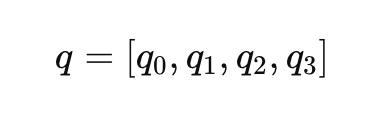
여기서 𝑞0은 스칼라 부분이고, [𝑞1, 𝑞2, 𝑞3]은 벡터 구성 요소입니다. 회전의 쿼터니언 표현은 다음과 같이 쓸 수 있습니다.
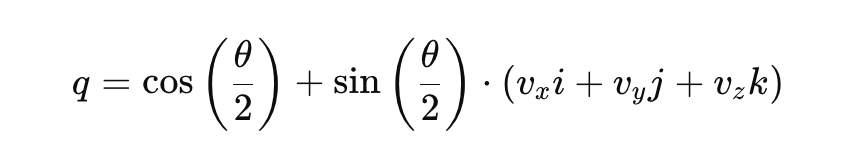
위치:
- θ는 회전 각도입니다.
- [vx,vy,vz]는 회전축을 나타내는 단위 벡터입니다.
- i, j, k 는 기본 쿼터니언 단위입니다.
쿼터니언(Quaternions)의 장점:
- 짐벌 락(Gimbal Lock) 및 특이점을 방지합니다.
- 보간에 있어 더욱 효율적인 연산이 가능합니다.
4 – 방향 여현 행렬(DCM)
방향 코사인 행렬은 회전 행렬과 유사하며 객체의 방향을 설명합니다. DCM은 한 프레임의 벡터 좌표를 다른 프레임의 동일한 벡터 좌표와 관련시킵니다.
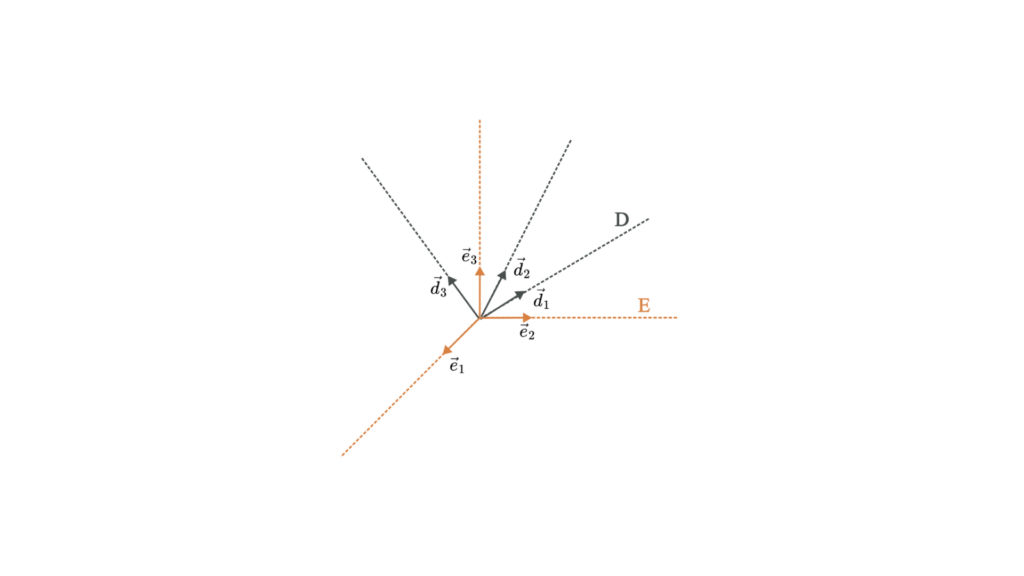
수학적 표현
방향 코사인 행렬 𝐶는 두 좌표 프레임 간의 관계를 정의하는 3×3 행렬입니다.
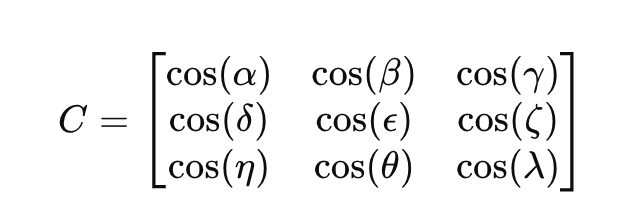
여기서 요소 cos (⋅)는 두 좌표 프레임 벡터 사이의 각도의 코사인을 나타냅니다.
프로젝트에 대해 알려주세요