El Filtro de Kalman Extendido (EKF) es una potente herramienta utilizada en sistemas de navegación y control para estimar el estado de un sistema que evoluciona con el tiempo. Es una extensión del Filtro de Kalman, diseñado para manejar sistemas no lineales, lo que lo hace crucial para aplicaciones donde la relación entre las variables no es lineal.
Este potente algoritmo se utiliza para estimar el estado de un sistema dinámico basándose en mediciones de sensores ruidosas. Se basa en el Filtro de Kalman estándar al admitir sistemas no lineales, que son comunes en escenarios de navegación del mundo real. Mientras que el Filtro de Kalman tradicional asume una dinámica lineal y un ruido gaussiano, el EKF supera estas limitaciones linealizando el sistema no lineal alrededor de la estimación actual. Esto le permite operar eficazmente en entornos más complejos de la vida real.
Principio básico del filtro de Kalman extendido
En esencia, el EKF actualiza continuamente un vector de estado, un conjunto de variables que describen la condición actual del sistema, como la posición, la velocidad y la orientación en contextos de navegación. Se basa en un modelo de proceso para predecir cómo evoluciona el estado con el tiempo, incorporando la dinámica del sistema y las entradas de control. Mientras tanto, el modelo de medición vincula los datos de los sensores entrantes al estado estimado, y una matriz de covarianza representa la incertidumbre tanto en las predicciones como en las observaciones, lo que ayuda al EKF a equilibrar la confianza entre las estimaciones del modelo y las entradas del sensor.
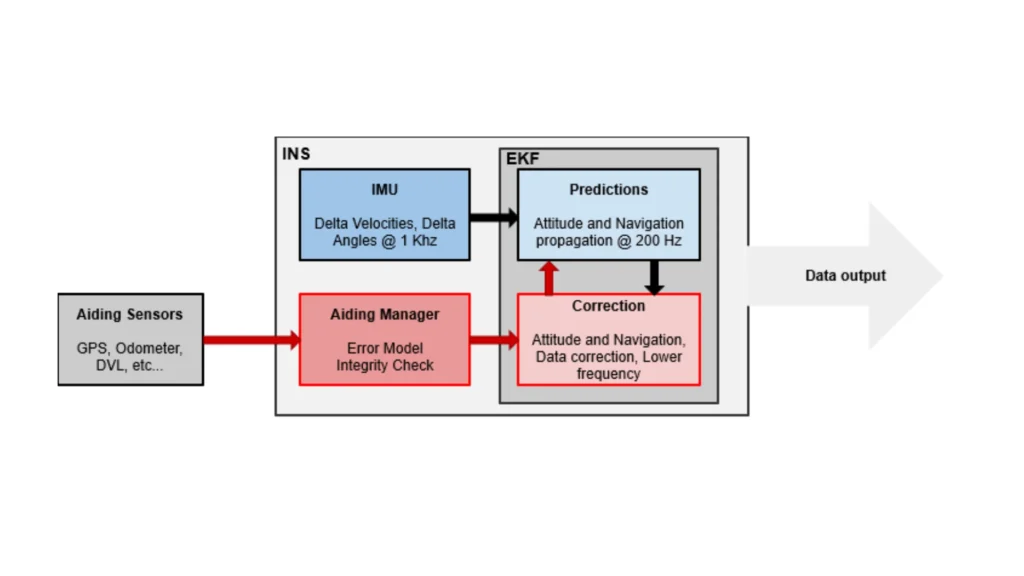
El filtro opera en dos fases principales: predicción y actualización. Durante la fase de predicción, utiliza el modelo de proceso para pronosticar el siguiente estado y predecir la incertidumbre asociada actualizando la matriz de covarianza. Para gestionar la no linealidad, el EKF linealiza tanto el proceso como los modelos de medición utilizando matrices jacobianas, representaciones matemáticas que aproximan cómo se comporta el sistema cerca de la estimación actual.
En la fase de actualización, el EKF incorpora nuevas mediciones de los sensores para refinar su predicción. Calcula la ganancia de Kalman, que determina cuánto peso asignar a las nuevas mediciones frente al estado predicho. Esta ganancia permite al EKF ajustar la estimación del estado en consecuencia y actualizar la covarianza para reflejar la incertidumbre reducida después de la medición.
Aplicación del EKF en aplicaciones modernas
El EKF se utiliza ampliamente en los sistemas de navegación modernos debido a su capacidad para ofrecer estimaciones precisas del estado en presencia de ruido y complejidad del sistema. Por ejemplo, los sistemas de navegación inercial (INS) se basan en acelerómetros y giroscopios, que son propensos a la deriva y al ruido. El EKF combina los datos de los sensores para proporcionar estimaciones estables de la posición, la velocidad y la orientación de las plataformas dinámicas. Estas estimaciones son fundamentales para el funcionamiento fiable de los vehículos autónomos, las aeronaves y otros sistemas móviles.
En robótica y sistemas autónomos, el EKF permite una localización y un mapeo robustos. Los robots utilizan sensores como LiDAR o cámaras para estimar la posición y actualizar los mapas mediante un filtro de Kalman extendido (EKF). Esto permite la cartografía y la localización en tiempo real, lo que favorece un funcionamiento seguro y autónomo en entornos desconocidos o dinámicos.
En el sector aeroespacial y de defensa, el EKF desempeña un papel fundamental en los sistemas de guiado y seguimiento. Permite a las aeronaves, los misiles y las naves espaciales mantener una posición y una trayectoria precisas, incluso en condiciones de movimiento no lineal. El EKF sigue funcionando de forma fiable cuando se expone a perturbaciones externas que, de otro modo, podrían degradar la precisión de la navegación.
La tecnología detrás del EKF incluye varios componentes críticos. Las matrices jacobianas apoyan el proceso de linealización, mientras que la fusión de sensores integra datos de múltiples fuentes para garantizar la resiliencia y la precisión. Para soportar el funcionamiento en tiempo real, el EKF depende de algoritmos computacionales eficientes para las operaciones matriciales, las actualizaciones de covarianza y la integración de mediciones.
En conclusión, el filtro de Kalman Extendido (EKF) es una herramienta esencial en los sistemas de navegación avanzados. Al extender el filtro de Kalman para manejar sistemas no lineales, se obtiene una estimación del estado precisa y en tiempo real. Es compatible con una amplia gama de aplicaciones, incluyendo la robótica, ADAS automotriz, la industria aeroespacial y los sistemas de defensa. Dominar los principios y las tecnologías del EKF es clave para desarrollar soluciones de navegación de alto rendimiento en entornos complejos y dinámicos.
