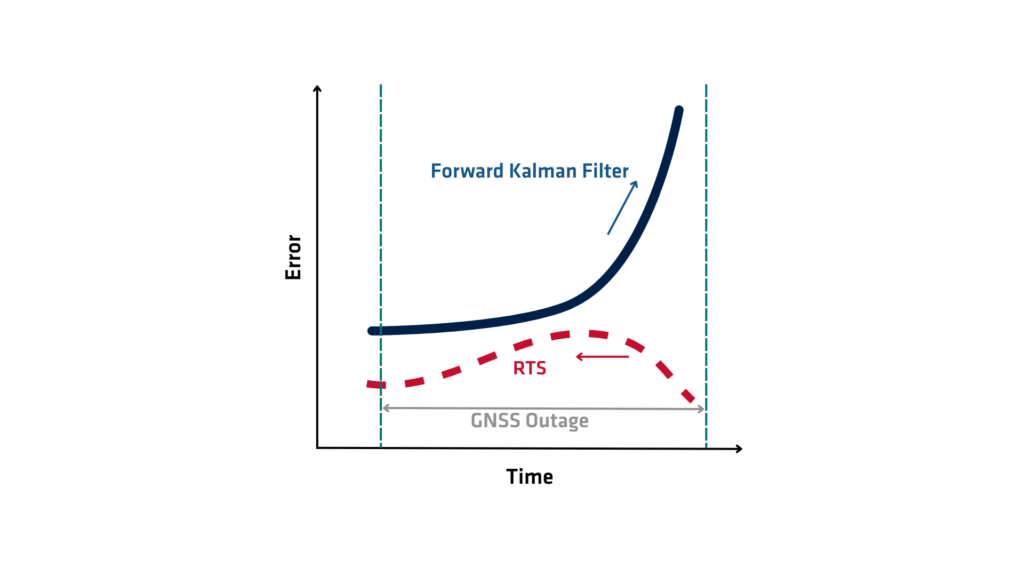
Der RTS-Smoother (Rauch-Tung-Striebel) ist ein mathematischer Algorithmus, der zur Verbesserung der Genauigkeit der Zustandsschätzung in dynamischen Systemen eingesetzt wird. Er gehört zur Familie der Glättungsalgorithmen und erweitert die Möglichkeiten des Kalman-Filters, das den Zustand eines Systems in Echtzeit schätzt. Während das Kalman-Filter Daten sequenziell verarbeitet und den aktuellen Zustand ausschließlich auf der Grundlage vergangener und gegenwärtiger Messungen schätzt, geht der RTS-Smoother noch einen Schritt weiter, indem er sowohl vergangene als auch zukünftige Messungen verwendet, um Zustandsschätzungen retrospektiv zu verfeinern. Dieser Prozess führt zu deutlich genaueren Zustandsschätzungen, insbesondere in Anwendungen, die eine Nachbearbeitung von Daten beinhalten.
Wie funktioniert RTS?
Der RTS-Smoother (Rauch-Tung-Striebel) arbeitet in zwei Hauptphasen: dem Vorwärtsdurchlauf und dem Rückwärtsdurchlauf. Während des Vorwärtsdurchlaufs führt der Algorithmus ein Standard-Kalman-Filter durch die Daten aus und erfasst Schätzungen des Zustands und der zugehörigen Fehlerkovarianzen zu jedem Zeitpunkt. Diese Phase legt im Wesentlichen den Grundstein, indem sie die anfänglichen Zustandsschätzungen und Unsicherheitsmaße liefert, die nur auf vergangenen Daten bis zu jedem Zeitpunkt basieren.
Sobald der Vorwärtsdurchlauf abgeschlossen ist, beginnt der Rückwärtsdurchlauf. Der Algorithmus arbeitet sich vom endgültigen Zustandsschätzer rückwärts zum anfänglichen Zustandsschätzer vor. Zu jedem Zeitpunkt korrigiert der RTS-Smoother (Rauch-Tung-Striebel) die Zustandsschätzung, indem er Informationen aus zukünftigen Zeitpunkten einbezieht–Informationen, die während des Vorwärtsfilterprozesses nicht verfügbar waren. Er verwendet den Kalman-Verstärkungsfaktor, Übergangsmatrizen und Kovarianzen, die im Vorwärtsdurchlauf berechnet wurden, um eine geglättete Schätzung zu berechnen, die sowohl vergangene als auch zukünftige Beobachtungen berücksichtigt. Diese Rückwärtsrekursion korrigiert die gefilterten Schätzungen, reduziert den Gesamtfehler der Schätzung und erzeugt eine konsistentere und genauere Trajektorie der Systemzustände.
Mathematisch wendet der Smoother einen Korrekturschritt an, der die Korrelation zwischen Fehlern in aufeinanderfolgenden Schätzungen nutzt. Durch die Modellierung der Systementwicklung durch einen linearen Gauß-Prozess geht der RTS-Smoother von den gleichen Dynamik- und Messmodellen aus, die im Kalman-Filter verwendet werden. Er berechnet in jedem Schritt einen Glättungsfaktor, der bestimmt, wie viel von der zukünftigen Schätzung zur Anpassung der aktuellen Schätzung verwendet werden soll. Dieser Faktor hängt von den Kovarianzmatrizen der gefilterten Schätzungen und dem vorhergesagten Zustand ab.
Vorteile von RTS (Rauch-Tung-Striebel)
Der RTS-Smoother erzeugt eine global optimale Schätzung für die gesamte Sequenz von Systemzuständen. Er geht davon aus, dass die Modelle linear und Gauß-verteilt sind. Die Filterung schätzt nur den aktuellen Zustand. Die Glättung rekonstruiert die besten Schätzungen des vergangenen Zustands unter Verwendung aller verfügbaren Daten. Dies macht die Glättung besonders wertvoll für Offline-Anwendungen.
Der RTS-Smoother findet Anwendung in verschiedenen Bereichen, darunter Luft- und Raumfahrtnavigation, Signalverarbeitung, Finanzen und Robotik. In Inertialnavigationssystemen (INS) wird er beispielsweise häufig zur Nachbearbeitung von Trajektoriendaten verwendet, um Drift und Rauschen zu reduzieren. In ähnlicher Weise wird er in der Zeitreihenanalyse oder Objektverfolgung verwendet, um Echtzeitschätzungen zu verfeinern und genaue Pfade oder Trends wiederherzustellen.
Der RTS-Smoother bietet Vorteile, benötigt aber vollen Zugriff auf den Datensatz und wird für lange oder komplexe Daten rechenintensiv. Er stützt sich auch stark auf die Annahme linearer Dynamik und Gaußschen Rauschens. Verwenden Sie den Extended oder Unscented RTS-Smoother, wenn das System nichtlinear ist oder das Rauschen nicht Gauß-verteilt ist. Diese Varianten passen die Methode an nichtlineare Filter wie den Extended Kalman Filter (EKF) oder den Unscented Kalman Filter (UKF) an.
Der RTS-Smoother verfeinert die Kalman-Filterung, indem er zukünftige Daten verwendet, um vergangene Schätzungen zu aktualisieren, wodurch die Genauigkeit und Stabilität verbessert werden. Er bildet die Grundlage der Zustandsschätzung und ermöglicht die präzise Rekonstruktion dynamischer Systeme mithilfe von nachbearbeiteten Daten.