Das Extended Kalman Filter (EKF) ist ein leistungsstarkes Werkzeug, das in Navigations- und Steuerungssystemen zur Schätzung des Zustands eines Systems verwendet wird, das sich im Laufe der Zeit entwickelt. Es handelt sich um eine Erweiterung des Kalman-Filters, die für den Umgang mit nichtlinearen Systemen entwickelt wurde und für Anwendungen, bei denen die Beziehung zwischen Variablen nichtlinear ist, von entscheidender Bedeutung ist.
Dieser leistungsstarke Algorithmus wird verwendet, um den Zustand eines dynamischen Systems auf der Grundlage verrauschter Sensormessungen zu schätzen. Er baut auf dem Standard-Kalman-Filter auf, indem er nichtlineare Systeme berücksichtigt, die in realen Navigationsszenarien üblich sind. Während der traditionelle Kalman-Filter lineare Dynamiken und Gaußsches Rauschen annimmt, überwindet der EKF diese Einschränkungen, indem er das nichtlineare System um die aktuelle Schätzung linearisiert. Dadurch kann er in komplexeren, realen Umgebungen effektiv arbeiten.
Grundprinzip des erweiterten Kalman-Filters
Im Kern aktualisiert der EKF kontinuierlich einen Zustandsvektor – eine Reihe von Variablen, die den aktuellen Zustand des Systems beschreiben, wie z. B. Position, Geschwindigkeit und Ausrichtung in Navigationskontexten. Er stützt sich auf ein Prozessmodell, um vorherzusagen, wie sich der Zustand im Laufe der Zeit entwickelt, wobei Systemdynamiken und Steuereingaben einbezogen werden. In der Zwischenzeit verknüpft das Messmodell eingehende Sensordaten mit dem geschätzten Zustand, und eine Kovarianzmatrix stellt die Unsicherheit sowohl bei Vorhersagen als auch bei Beobachtungen dar, wodurch der EKF das Vertrauen zwischen Modellschätzungen und Sensoreingaben ausbalanciert.
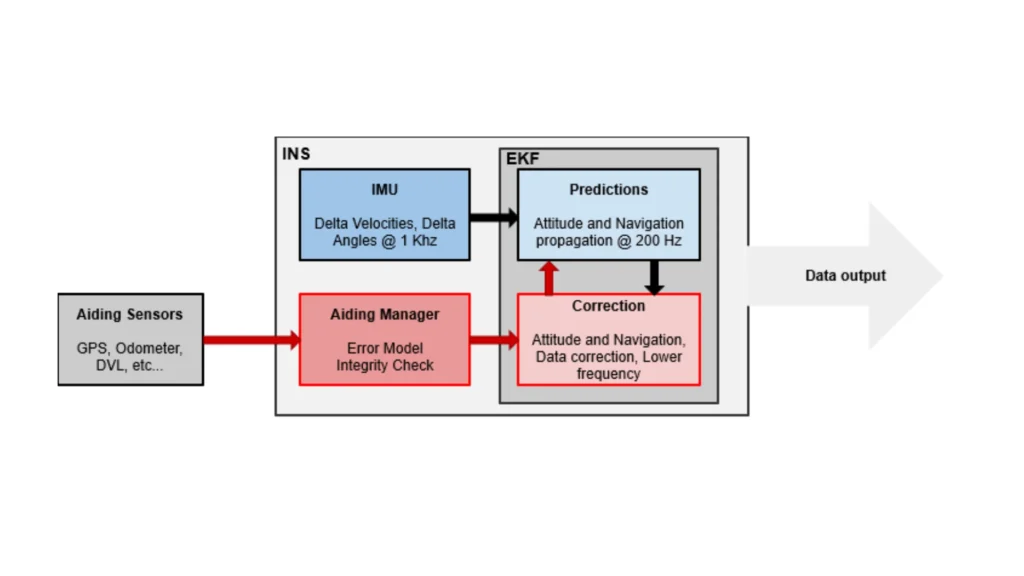
Der Filter arbeitet in zwei Hauptphasen: Vorhersage und Aktualisierung. Während der Vorhersagephase verwendet er das Prozessmodell, um den nächsten Zustand vorherzusagen und die damit verbundene Unsicherheit durch Aktualisierung der Kovarianzmatrix vorherzusagen. Um die Nichtlinearität zu bewältigen, linearisiert der EKF sowohl das Prozess- als auch das Messmodell mithilfe von Jacobi-Matrizen – mathematische Darstellungen, die annähern, wie sich das System in der Nähe der aktuellen Schätzung verhält.
In der Aktualisierungsphase bezieht der EKF neue Sensormessungen ein, um seine Vorhersage zu verfeinern. Er berechnet den Kalman-Gain, der bestimmt, wie viel Gewicht den neuen Messungen im Vergleich zum vorhergesagten Zustand beigemessen werden soll. Dieser Gain ermöglicht es dem EKF, die Zustandsschätzung entsprechend anzupassen und die Kovarianz zu aktualisieren, um die reduzierte Unsicherheit nach der Messung widerzuspiegeln.
Anwendung des EKF in modernen Anwendungen
Der EKF wird aufgrund seiner Fähigkeit, genaue Zustandsschätzungen in Gegenwart von Rauschen und Systemkomplexität zu liefern, in modernen Navigationssystemen häufig eingesetzt. Beispielsweise sind Inertial Navigation Systems (INS) auf Beschleunigungsmesser und Gyroskope angewiesen, die anfällig für Drift und Rauschen sind. Der EKF kombiniert Sensordaten, um stabile Schätzungen von Position, Geschwindigkeit und Orientierung für dynamische Plattformen bereitzustellen. Diese Schätzungen sind entscheidend für den zuverlässigen Betrieb von autonomen Fahrzeugen, Flugzeugen und anderen mobilen Systemen.
In der Robotik und in autonomen Systemen ermöglicht der EKF eine robuste Lokalisierung und Kartierung. Roboter verwenden Sensoren wie LiDAR oder Kameras, um die Position zu schätzen und Karten mithilfe eines Extended Kalman Filter (EKF) zu aktualisieren. Dies ermöglicht eine Echtzeit-Kartierung und -Lokalisierung und unterstützt einen sicheren und autonomen Betrieb in unbekannten oder dynamischen Umgebungen.
In der Luft- und Raumfahrt sowie im Verteidigungsbereich spielt der EKF eine wichtige Rolle in Leit- und Verfolgungssystemen. Er ermöglicht es Flugzeugen, Raketen und Raumfahrzeugen, eine präzise Position und Flugbahn beizubehalten, selbst unter nichtlinearen Bewegungsbedingungen. Der EKF arbeitet weiterhin zuverlässig, wenn er externen Störungen ausgesetzt ist, die andernfalls die Navigationsgenauigkeit beeinträchtigen könnten.
Die Technologie hinter dem EKF umfasst mehrere kritische Komponenten. Jacobi-Matrizen unterstützen den Linearisierungsprozess, während die Sensorfusion Daten aus mehreren Quellen integriert, um Widerstandsfähigkeit und Genauigkeit zu gewährleisten. Um den Echtzeitbetrieb zu unterstützen, ist der EKF auf effiziente Berechnungsalgorithmen für Matrixoperationen, Kovarianzaktualisierungen und Messintegration angewiesen.
Zusammenfassend lässt sich sagen, dass der Extended Kalman Filter (EKF) ein wesentliches Werkzeug in modernen Navigationssystemen ist. Durch die Erweiterung des Kalman-Filters zur Verarbeitung nichtlinearer Systeme erhalten Sie eine genaue Zustandsschätzung in Echtzeit. Er unterstützt eine breite Palette von Anwendungen, darunter Robotik, automotive ADAS, Luft- und Raumfahrt sowie Verteidigungssysteme. Die Beherrschung der Prinzipien und Technologien des EKF ist der Schlüssel zur Entwicklung von Hochleistungs-Navigationslösungen in komplexen und dynamischen Umgebungen.
