Le lisseur RTS (Rauch-Tung-Striebel) est un algorithme mathématique utilisé pour améliorer la précision de l'estimation d'état dans les systèmes dynamiques. Il appartient à la famille des algorithmes de lissage et étend les capacités du filtre de Kalman, qui estime l'état d'un système en temps réel. Alors que le filtre de Kalman traite les données de manière séquentielle et estime l'état actuel uniquement sur la base des mesures passées et présentes, le lisseur RTS va plus loin en utilisant à la fois les mesures passées et futures pour affiner rétrospectivement les estimations d'état. Ce processus se traduit par des estimations d'état beaucoup plus précises, en particulier dans les applications qui impliquent le post-traitement des données.
Comment fonctionne le RTS ?
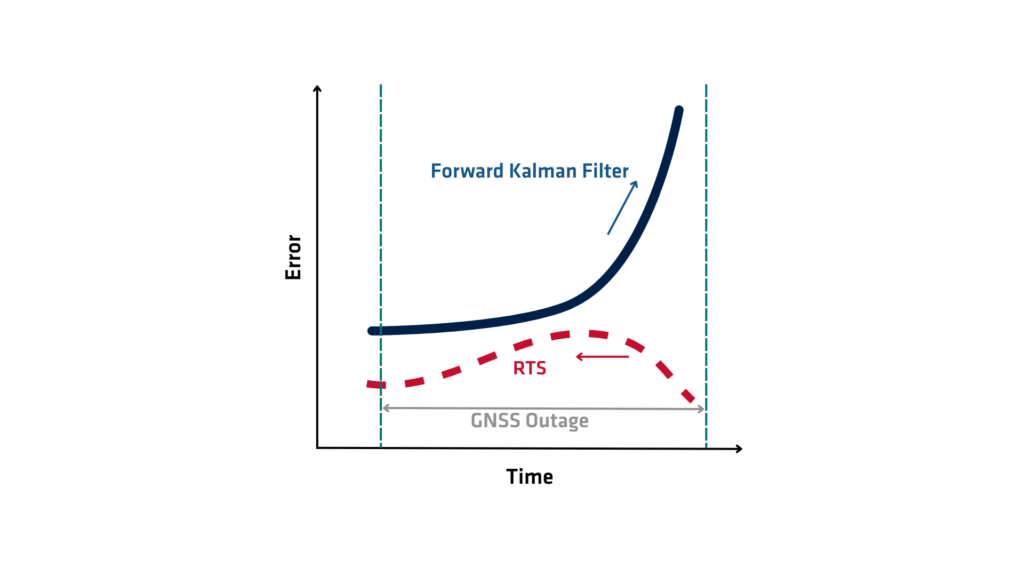
Le lisseur RTS (Rauch-Tung-Striebel) fonctionne en deux étapes principales : le passage aller et le passage retour. Lors du passage aller, l’algorithme exécute un filtre de Kalman standard à travers les données, en collectant des estimations de l’état et des covariances d’erreur associées à chaque pas de temps. Cette étape jette essentiellement les bases en fournissant les estimations d’état initiales et les mesures d’incertitude, basées uniquement sur les données passées jusqu’à chaque point dans le temps.
Une fois le passage aller terminé, le passage retour commence. L’algorithme remonte à partir de l’estimation de l’état final vers l’estimation initiale. À chaque pas de temps, le lisseur RTS (Rauch-Tung-Striebel) révise l’estimation de l’état en incorporant des informations provenant des pas de temps futurs, informations qui n’étaient pas disponibles pendant le processus de filtrage aller. Il utilise le gain de Kalman, les matrices de transition et les covariances calculées lors du passage aller pour calculer une estimation lissée qui équilibre les observations passées et futures. Cette récursion vers l’arrière corrige les estimations filtrées, réduisant ainsi l’erreur d’estimation globale et produisant une trajectoire plus cohérente et précise des états du système.
Mathématiquement, le lisseur applique une étape de correction qui exploite la corrélation entre les erreurs dans les estimations successives. En modélisant l’évolution du système à travers un processus gaussien linéaire, le lisseur RTS suppose les mêmes modèles de dynamique et de mesure que ceux utilisés dans le filtre de Kalman. Il calcule un gain de lissage à chaque étape, qui détermine la part de l’estimation future qui doit être utilisée pour ajuster l’estimation actuelle. Ce gain dépend des matrices de covariance des estimations filtrées et de l’état prédit.
Avantages du lisseur RTS (Rauch-Tung-Striebel)
Le filtre lisseur RTS produit une estimation globalement optimale pour l'ensemble de la séquence des états du système. Il suppose que les modèles sont linéaires et gaussiens. Le filtrage estime uniquement l'état actuel. Le lissage reconstruit les meilleures estimations de l'état passé en utilisant toutes les données disponibles. Cela rend le lissage particulièrement utile pour les applications hors ligne.
Le filtre lisseur RTS trouve son application dans divers domaines, notamment la navigation aérospatiale, le traitement du signal, la finance et la robotique. Dans les systèmes de navigation inertielle (INS), par exemple, il est souvent utilisé pour post-traiter les données de trajectoire afin de réduire la dérive et le bruit. De même, l'analyse des séries chronologiques ou le suivi d'objets l'utilise pour affiner les estimations en temps réel et récupérer des chemins ou des tendances précis.
Le filtre lisseur RTS offre des avantages, mais nécessite un accès complet à l'ensemble de données et devient gourmand en calculs pour les données longues ou complexes. Il repose également fortement sur l'hypothèse d'une dynamique linéaire et d'un bruit gaussien. Utilisez le filtre lisseur RTS étendu ou non parfumé lorsque le système est non linéaire ou que le bruit est non gaussien. Ces variantes adaptent la méthode aux filtres non linéaires comme le filtre de Kalman étendu (EKF) ou le filtre de Kalman non parfumé (UKF).
Le filtre lisseur RTS affine le filtrage de Kalman en utilisant les données futures pour mettre à jour les estimations passées, améliorant ainsi la précision et la stabilité. Il constitue la base de l'estimation d'état et permet une reconstruction précise des systèmes dynamiques à l'aide de données post-traitées.