RTS(Rauch-Tung-Striebel)平滑器是一种数学算法,用于提高动态系统中状态估计的准确性。它属于平滑算法系列,并扩展了卡尔曼滤波器的功能,卡尔曼滤波器实时估计系统的状态。虽然卡尔曼滤波器按顺序处理数据并仅根据过去和现在的测量值来估计当前状态,但 RTS 平滑器通过使用过去和未来的测量值来追溯地细化状态估计,从而更进一步。此过程会产生明显更准确的状态估计,尤其是在涉及数据后处理的应用程序中。
RTS 如何工作?
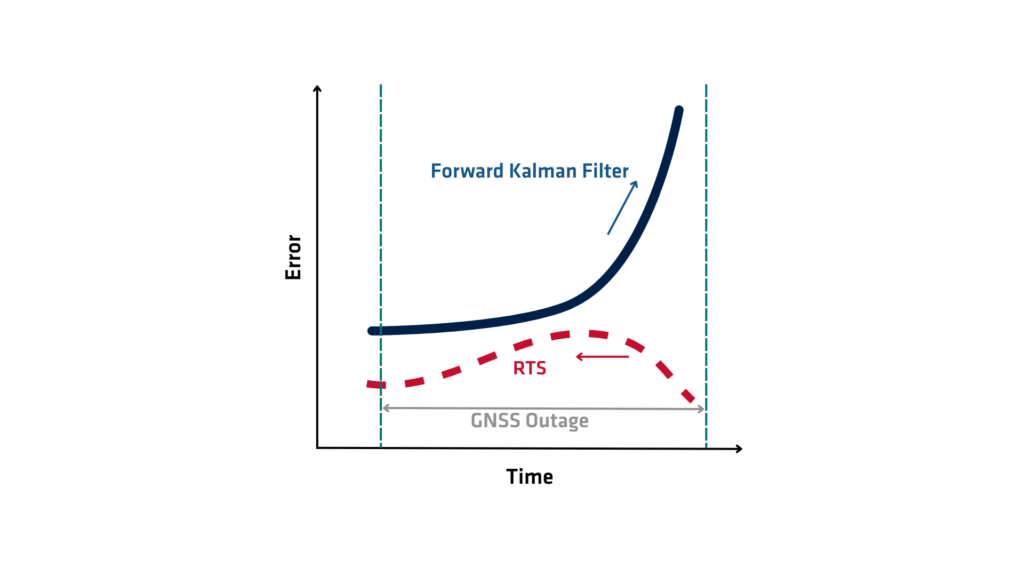
RTS(Rauch-Tung-Striebel)或 RTS 平滑器在两个主要阶段运行:前向传递和后向传递。在前向传递期间,该算法通过数据运行标准卡尔曼滤波器,收集每个时间步的状态估计和相关的误差协方差。此阶段本质上是通过仅基于截至每个时间点之前的过去数据提供初始状态估计和不确定性度量来奠定基础。
前向传递完成后,后向传递开始。该算法从最终状态估计向初始状态估计向后工作。在每个时间步,RTS(Rauch-Tung-Striebel)通过合并来自未来时间步的信息(在前向滤波过程中无法获得的信息)来修正状态估计。它使用在前向传递中计算的卡尔曼增益、转移矩阵和协方差来计算平滑估计,该估计平衡了过去和未来的观测结果。这种后向递归校正了滤波后的估计,减少了总体估计误差,并生成了系统状态的更一致和准确的轨迹
在数学上,平滑器应用了一个校正步骤,该步骤利用了连续估计中误差之间的相关性。通过对通过线性高斯过程的系统演化进行建模,RTS 平滑器假定卡尔曼滤波器中使用的相同动力学和测量模型。它在每个步骤计算一个平滑增益,该增益确定应使用多少未来估计来调整当前估计。此增益取决于滤波后估计的协方差矩阵和预测状态。
RTS(Rauch-Tung-Striebel)的优势
RTS 平滑器为整个系统状态序列生成全局最优估计。它假设模型是线性和高斯分布的。滤波仅估计当前状态。平滑使用所有可用数据重建最佳过去状态估计。这使得平滑对于离线应用尤其有价值。
RTS 平滑器可应用于各种领域,包括航空航天导航、信号处理、金融和机器人技术。例如,在惯性导航系统 (INS) 中,它通常用于后处理轨迹数据,以减少漂移和噪声。同样,时间序列分析或对象跟踪使用它来改进实时估计并恢复准确的路径或趋势。
RTS 平滑器具有优势,但需要完全的数据集访问权限,并且对于长数据或复杂数据,计算量会变得很大。它还严重依赖于线性动力学和高斯噪声的假设。当系统是非线性或噪声是非高斯分布时,请使用扩展或无迹 RTS 平滑器。这些变体将该方法调整为非线性滤波器,如扩展卡尔曼滤波器 (EKF) 或无迹卡尔曼滤波器 (UKF)。
RTS 平滑器通过使用未来数据更新过去估计来改进卡尔曼滤波,从而提高精度和稳定性。它构成了状态估计的基础,并可以使用后处理数据精确重建动态系统。