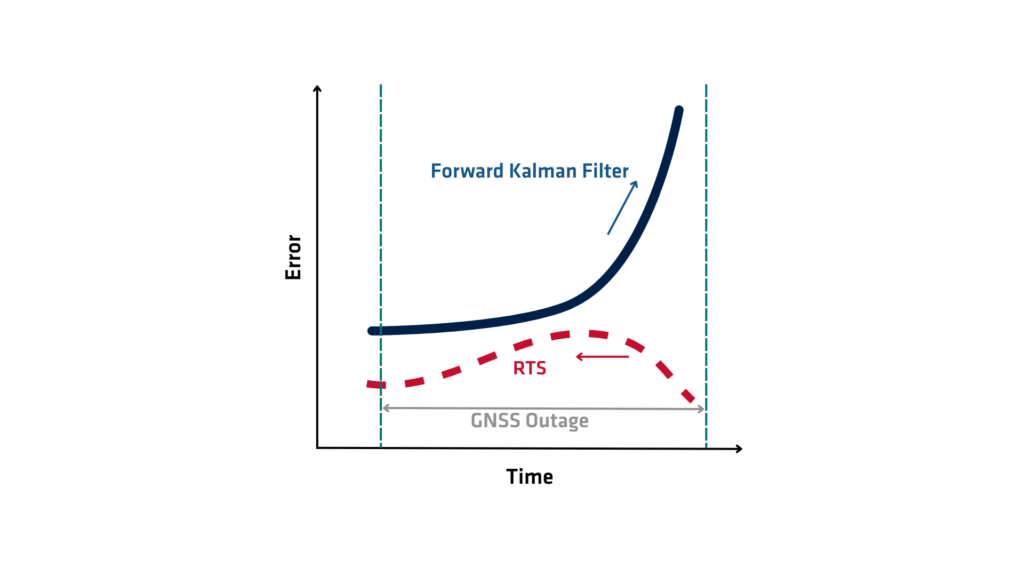
RTS (Rauch-Tung-Striebel) 스무더는 동적 시스템에서 상태 추정의 정확도를 향상시키는 데 사용되는 수학적 알고리즘입니다. 이는 평활화 알고리즘 계열에 속하며 실시간으로 시스템의 상태를 추정하는 칼만 필터의 기능을 확장합니다. 칼만 필터는 데이터를 순차적으로 처리하고 과거 및 현재 측정값만을 기반으로 현재 상태를 추정하는 반면, RTS 스무더는 과거 및 미래 측정값을 모두 사용하여 상태 추정치를 소급하여 개선함으로써 한 단계 더 나아갑니다. 이 프로세스는 특히 데이터 사후 처리가 필요한 애플리케이션에서 훨씬 더 정확한 상태 추정을 제공합니다.
RTS는 어떻게 작동하나요?
RTS (Rauch-Tung-Striebel) smoother 또는 RTS 스무더는 순방향 패스와 역방향 패스라는 두 가지 주요 단계로 작동합니다. 순방향 패스 동안 알고리즘은 표준 칼만 필터를 통해 데이터를 실행하여 각 시간 단계에서 상태 및 관련 오차 공분산에 대한 추정치를 수집합니다. 이 단계는 기본적으로 각 시점까지의 과거 데이터만을 기반으로 초기 상태 추정치와 불확실성 측정값을 제공하여 토대를 마련합니다.
순방향 패스가 완료되면 역방향 패스가 시작됩니다. 알고리즘은 최종 상태 추정치에서 초기 상태 추정치 방향으로 역방향으로 진행됩니다. 각 시간 단계에서 RTS (Rauch-Tung-Striebel)는 미래 시간 단계의 정보(순방향 필터링 프로세스 동안에는 사용할 수 없었던 정보)를 통합하여 상태 추정치를 수정합니다. 순방향 패스에서 계산된 칼만 이득, 전이 행렬 및 공분산을 사용하여 과거 및 미래 관측치의 균형을 맞추는 평활화된 추정치를 계산합니다. 이 역방향 재귀는 필터링된 추정치를 수정하여 전체 추정 오차를 줄이고 시스템 상태의 보다 일관되고 정확한 궤적을 생성합니다.
수학적으로 스무더는 연속적인 추정치의 오차 간의 상관 관계를 활용하는 수정 단계를 적용합니다. 선형 가우시안 프로세스를 통해 시스템의 진화를 모델링함으로써 RTS 스무더는 칼만 필터에서 사용되는 것과 동일한 역학 및 측정 모델을 가정합니다. 각 단계에서 평활화 이득을 계산하여 현재 추정치를 조정하는 데 미래 추정치를 얼마나 사용해야 하는지 결정합니다. 이 이득은 필터링된 추정치의 공분산 행렬과 예측된 상태에 따라 달라집니다.
RTS (Rauch-Tung-Striebel)의 장점
RTS 스무더는 전체 시스템 상태 시퀀스에 대한 전역적으로 최적의 추정치를 생성합니다. 모델이 선형이고 가우스 분포를 따른다고 가정합니다. 필터링은 현재 상태만 추정합니다. 스무딩은 사용 가능한 모든 데이터를 사용하여 최상의 과거 상태 추정치를 재구성합니다. 따라서 스무딩은 오프라인 애플리케이션에 특히 유용합니다.
RTS 스무더는 항공우주 항법, 신호 처리, 금융 및 로봇 공학을 포함한 다양한 영역에서 응용됩니다. 예를 들어 관성 항법 시스템(INS)에서는 궤적 데이터를 사후 처리하여 드리프트 및 노이즈를 줄이는 데 자주 사용됩니다. 마찬가지로 시계열 분석 또는 객체 추적에서는 실시간 추정치를 개선하고 정확한 경로 또는 추세를 복구하는 데 사용됩니다.
RTS 스무더는 장점을 제공하지만 전체 데이터 세트에 대한 액세스가 필요하며 데이터가 길거나 복잡한 경우 계산 집약적이 됩니다. 또한 선형 역학 및 가우스 노이즈에 대한 가정에 크게 의존합니다. 시스템이 비선형이거나 노이즈가 비가우스 분포를 따르는 경우 확장 또는 Unscented RTS 스무더를 사용하십시오. 이러한 변형은 확장 칼만 필터(EKF) 또는 Unscented 칼만 필터(UKF)와 같은 비선형 필터에 맞게 방법을 조정합니다.
RTS 스무더는 과거 추정치를 업데이트하기 위해 미래 데이터를 사용하여 칼만 필터링을 개선하여 정확도와 안정성을 향상시킵니다. 이는 상태 추정의 기초를 형성하고 사후 처리된 데이터를 사용하여 동적 시스템을 정밀하게 재구성할 수 있도록 합니다.