拡張カルマンフィルター(EKF)は、時間とともに変化するシステムの状態を推定するために、ナビゲーションおよび制御システムで使用される強力なツールです。カルマンフィルターの拡張であり、非線形システムを処理するように設計されているため、変数間の関係が線形ではないアプリケーションに不可欠です。
この強力なアルゴリズムは、ノイズの多いセンサー測定に基づいて動的システムの状態を推定するために使用されます。標準的なカルマンフィルターを基に構築されており、実際のナビゲーションシナリオで一般的な非線形システムに対応しています。従来のカルマンフィルターは線形ダイナミクスとガウスノイズを仮定していますが、EKFは現在の推定値の周りで非線形システムを線形化することにより、これらの制限を克服します。これにより、より複雑な実際の環境で効果的に動作できます。
拡張カルマンフィルターの基本原理
EKFの中核となるのは、状態ベクトル(航法における位置、速度、姿勢など、システムの状態を表す一連の変数)を継続的に更新することです。状態が時間とともにどのように変化するかを予測するために、プロセスモデルを利用し、システムのダイナミクスと制御入力を組み込みます。一方、計測モデルは、入ってくるセンサーデータを推定された状態にリンクさせ、共分散行列は、予測と観測の両方における不確実性を表し、EKFがモデル推定とセンサー入力の間の信頼性のバランスを取るのに役立ちます。
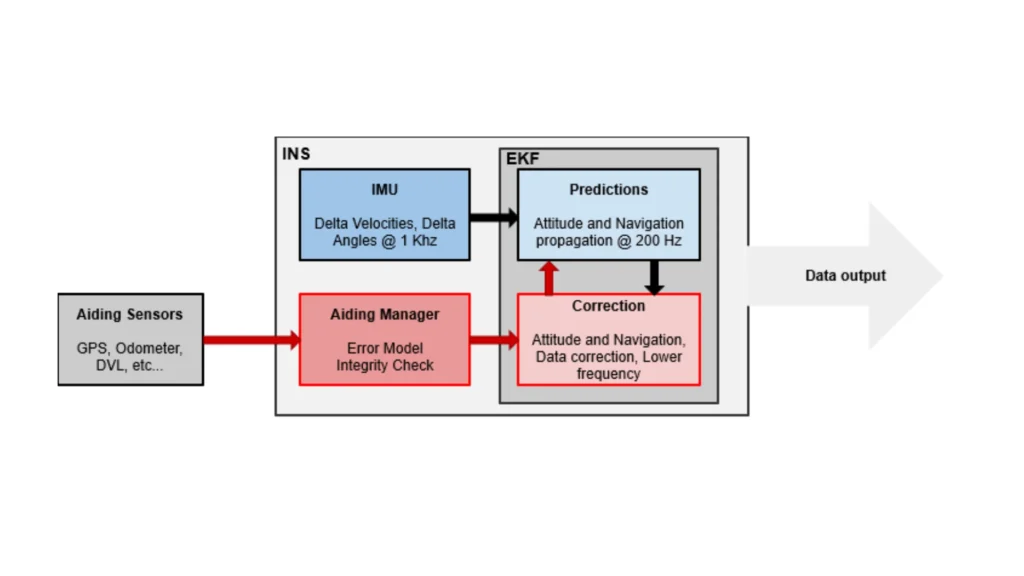
フィルターは、予測と更新の2つの主要なフェーズで動作します。予測フェーズでは、プロセスモデルを使用して次の状態を予測し、共分散行列を更新することにより、関連する不確実性を予測します。非線形性を管理するために、EKFは、現在の推定値付近でのシステムの動作を近似する数学的表現であるヤコビ行列を使用して、プロセスモデルと測定モデルの両方を線形化します。
更新フェーズでは、EKFは新しいセンサー測定値を組み込んで、予測を改善します。新しい測定値と予測された状態に割り当てる重みを決定するカルマンゲインを計算します。このゲインにより、EKFは状態推定値をそれに応じて調整し、測定後の不確実性の低減を反映するように共分散を更新できます。
現代のアプリケーションにおけるEKFの適用
EKFは、ノイズやシステムの複雑さがある状況下でも正確な状態推定を提供できるため、最新のナビゲーションシステムで広く使用されています。たとえば、慣性航法システム(INS)は、ドリフトやノイズが発生しやすい加速度計とジャイロスコープに依存しています。EKFはセンサーデータを組み合わせて、動的プラットフォームの位置、速度、および姿勢の安定した推定を提供します。これらの推定は、自律走行車、航空機、その他のモバイルシステムの信頼性の高い動作に不可欠です。
ロボット工学および自律システムでは、EKFは堅牢なローカリゼーションとマッピングを可能にします。ロボットは、LiDARやカメラなどのセンサーを使用して位置を推定し、拡張カルマンフィルター(EKF)を使用してマップを更新します。これにより、リアルタイムのマッピングとローカリゼーションが可能になり、不慣れな環境または動的な環境での安全で自律的な操作がサポートされます。
航空宇宙および防衛では、EKFは誘導および追跡システムにおいて重要な役割を果たします。これにより、航空機、ミサイル、宇宙船は、非線形運動条件下でも正確な位置と軌道を維持できます。EKFは、ナビゲーションの精度を低下させる可能性のある外部からの妨害にさらされても、確実に動作し続けます。
EKFの背景にある技術には、いくつかの重要なコンポーネントが含まれています。ヤコビ行列は線形化プロセスをサポートし、センサーフュージョンは複数のソースからのデータを統合して、耐性と精度を確保します。リアルタイム動作をサポートするために、EKFは、行列演算、共分散の更新、および測定統合のための効率的な計算アルゴリズムに依存しています。
結論として、拡張カルマンフィルター(EKF)は、高度なナビゲーションシステムに不可欠なツールです。カルマンフィルターを拡張して非線形システムを処理することで、正確でリアルタイムな状態推定が可能になります。ロボット工学、自動車ADAS、航空宇宙、防衛システムなど、幅広いアプリケーションをサポートします。複雑で動的な環境で高性能なナビゲーションソリューションを開発するには、EKFの原理と技術を習得することが重要です。
