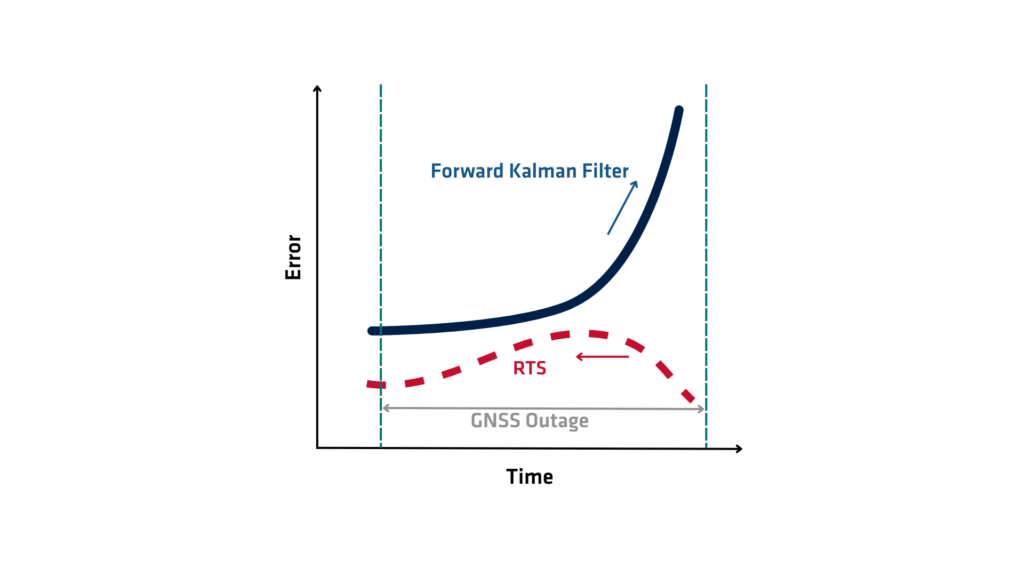
O suavizador RTS (Rauch-Tung-Striebel) é um algoritmo matemático usado para melhorar a precisão da estimativa de estado em sistemas dinâmicos. Ele pertence à família de algoritmos de suavização e estende os recursos do filtro de Kalman, que estima o estado de um sistema em tempo real. Enquanto o filtro de Kalman processa os dados sequencialmente e estima o estado atual com base apenas em medições passadas e presentes, o suavizador RTS vai um passo além, usando medições passadas e futuras para refinar as estimativas de estado retrospectivamente. Este processo resulta em estimativas de estado significativamente mais precisas, especialmente em aplicações que envolvem o pós-processamento de dados.
Como funciona o RTS?
O suavizador RTS (Rauch-Tung-Striebel) opera em dois estágios principais: o passo de avanço e o passo de retrocesso. Durante o passo de avanço, o algoritmo executa um filtro de Kalman padrão através dos dados, coletando estimativas do estado e covariâncias de erro associadas em cada etapa de tempo. Este estágio essencialmente estabelece as bases, fornecendo as estimativas de estado iniciais e medidas de incerteza, com base apenas em dados passados até cada ponto no tempo.
Uma vez que o passo de avanço é concluído, o passo de retrocesso começa. O algoritmo funciona retrocedendo da estimativa do estado final em direção à inicial. Em cada etapa de tempo, o RTS (Rauch-Tung-Striebel) revisa a estimativa do estado, incorporando informações de etapas de tempo futuras – informações que não estavam disponíveis durante o processo de filtragem de avanço. Ele usa o ganho de Kalman, as matrizes de transição e as covariâncias calculadas no passo de avanço para calcular uma estimativa suavizada que equilibra as observações passadas e futuras. Essa recursão para trás corrige as estimativas filtradas, reduzindo o erro geral de estimativa e produzindo uma trajetória mais consistente e precisa dos estados do sistema.
Matematicamente, o suavizador aplica uma etapa de correção que aproveita a correlação entre erros em estimativas sucessivas. Ao modelar a evolução do sistema por meio de um processo Gaussiano linear, o suavizador RTS assume a mesma dinâmica e modelos de medição usados no filtro de Kalman. Ele calcula um ganho de suavização em cada etapa, que determina a quantidade da estimativa futura que deve ser usada para ajustar a estimativa atual. Esse ganho depende das matrizes de covariância das estimativas filtradas e do estado previsto.
Vantagens do RTS (Rauch-Tung-Striebel)
O suavizador RTS produz uma estimativa globalmente ideal para toda a sequência de estados do sistema. Ele assume que os modelos são lineares e Gaussianos. A filtragem estima apenas o estado atual. A suavização reconstrói as melhores estimativas de estado passadas usando todos os dados disponíveis. Isso torna a suavização especialmente valiosa para aplicações offline.
O suavizador RTS encontra aplicação em vários domínios, incluindo navegação aeroespacial, processamento de sinais, finanças e robótica. Em sistemas de navegação inercial (INS), por exemplo, é frequentemente usado para pós-processar dados de trajetória para reduzir desvios e ruídos. Da mesma forma, a análise de séries temporais ou o rastreamento de objetos o utiliza para refinar estimativas em tempo real e recuperar caminhos ou tendências precisos.
O suavizador RTS oferece vantagens, mas precisa de acesso total ao conjunto de dados e torna-se computacionalmente intensivo para dados longos ou complexos. Ele também depende fortemente da suposição de dinâmica linear e ruído Gaussiano. Use o suavizador RTS Estendido ou Não-centrado quando o sistema for não linear ou o ruído for não Gaussiano. Essas variantes adaptam o método a filtros não lineares, como o Filtro de Kalman Estendido (EKF) ou o Filtro de Kalman Não-centrado (UKF).
O suavizador RTS refina a filtragem de Kalman usando dados futuros para atualizar estimativas passadas, melhorando a precisão e a estabilidade. Ele forma a base da estimativa de estado e permite a reconstrução precisa de sistemas dinâmicos usando dados pós-processados.