O Filtro de Kalman Estendido (EKF) é uma ferramenta poderosa usada em sistemas de navegação e controle para estimar o estado de um sistema que evolui ao longo do tempo. É uma extensão do Filtro de Kalman, projetado para lidar com sistemas não lineares, tornando-o crucial para aplicações onde a relação entre as variáveis não é linear.
Este poderoso algoritmo é usado para estimar o estado de um sistema dinâmico com base em medições de sensores ruidosas. Ele se baseia no Filtro de Kalman padrão, acomodando sistemas não lineares, que são comuns em cenários de navegação do mundo real. Enquanto o Filtro de Kalman tradicional assume dinâmica linear e ruído gaussiano, o EKF supera essas limitações linearizando o sistema não linear em torno da estimativa atual. Isso permite que ele opere de forma eficaz em ambientes mais complexos da vida real.
Princípio básico do filtro de Kalman estendido
Em sua essência, o EKF atualiza continuamente um vetor de estado — um conjunto de variáveis que descrevem a condição atual do sistema, como posição, velocidade e orientação em contextos de navegação. Ele se baseia em um modelo de processo para prever como o estado evolui ao longo do tempo, incorporando a dinâmica do sistema e as entradas de controle. Enquanto isso, o modelo de medição vincula os dados do sensor de entrada ao estado estimado, e uma matriz de covariância representa a incerteza nas previsões e observações, ajudando o EKF a equilibrar a confiança entre as estimativas do modelo e as entradas do sensor.
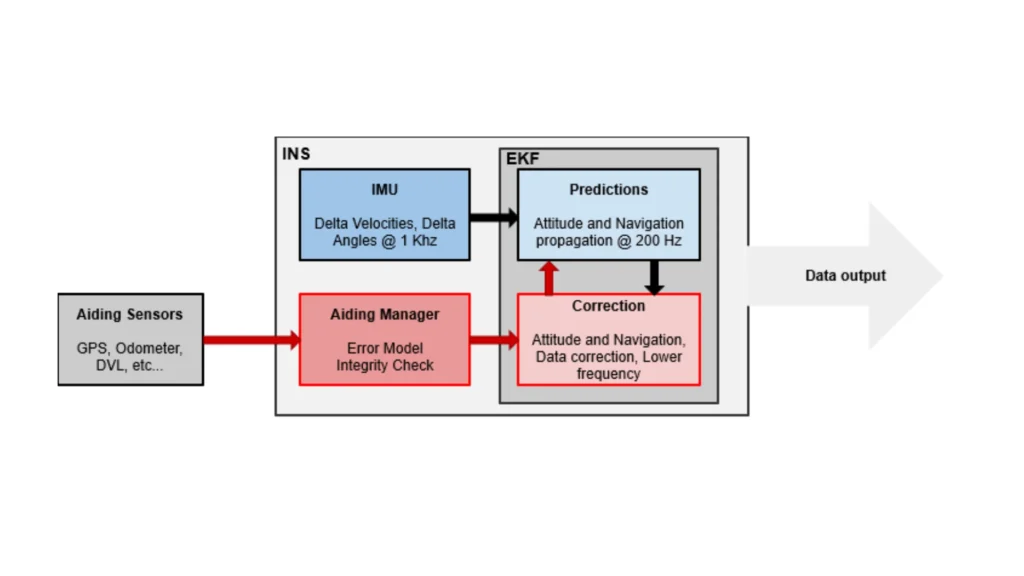
O filtro opera em duas fases principais: predição e atualização. Durante a fase de predição, ele usa o modelo de processo para prever o próximo estado e prever a incerteza associada, atualizando a matriz de covariância. Para gerenciar a não linearidade, o EKF lineariza os modelos de processo e medição usando matrizes Jacobianas — representações matemáticas que aproximam como o sistema se comporta perto da estimativa atual.
Na fase de atualização, o EKF incorpora novas medições do sensor para refinar sua predição. Ele calcula o Ganho de Kalman, que determina quanto peso atribuir às novas medições em relação ao estado previsto. Este ganho permite que o EKF ajuste a estimativa do estado de acordo e atualize a covariância para refletir a incerteza reduzida após a medição.
Aplicando o EKF em aplicações modernas
O EKF é amplamente utilizado em sistemas de navegação modernos devido à sua capacidade de fornecer estimativas de estado precisas na presença de ruído e complexidade do sistema. Por exemplo, os Sistemas de Navegação Inercial (INS) dependem de acelerômetros e giroscópios, que são propensos a desvios e ruídos. O EKF combina dados de sensores para fornecer estimativas estáveis de posição, velocidade e orientação para plataformas dinâmicas. Essas estimativas são críticas para a operação confiável de veículos autônomos, aeronaves e outros sistemas móveis.
Em robótica e sistemas autônomos, o EKF permite a localização e o mapeamento robustos. Os robôs usam sensores como LiDAR ou câmeras para estimar a posição e atualizar os mapas usando um Filtro de Kalman Estendido (EKF). Isso permite o mapeamento e a localização em tempo real, oferecendo suporte à operação segura e autônoma em ambientes desconhecidos ou dinâmicos.
No setor aeroespacial e de defesa, o EKF desempenha um papel vital nos sistemas de orientação e rastreamento. Ele permite que aeronaves, mísseis e espaçonaves mantenham uma posição e trajetória precisas, mesmo sob condições de movimento não linear. O EKF continua a operar de forma confiável quando exposto a distúrbios externos que, de outra forma, poderiam degradar a precisão da navegação.
A tecnologia por trás do EKF inclui vários componentes críticos. As matrizes Jacobian suportam o processo de linearização, enquanto a fusão de sensores integra dados de várias fontes para garantir resiliência e precisão. Para suportar a operação em tempo real, o EKF depende de algoritmos computacionais eficientes para operações de matrizes, atualizações de covariância e integração de medições.
Em conclusão, o filtro de Kalman estendido (EKF) é uma ferramenta essencial em sistemas de navegação avançados. Ao estender o filtro de Kalman para lidar com sistemas não lineares, você obtém uma estimativa de estado precisa e em tempo real. Ele oferece suporte a uma ampla gama de aplicações, incluindo robótica, ADAS automotivo, aeroespacial e sistemas de defesa. Dominar os princípios e as tecnologias do EKF é fundamental para desenvolver soluções de navegação de alto desempenho em ambientes complexos e dinâmicos.
