Lo smoother RTS (Rauch-Tung-Striebel) è un algoritmo matematico utilizzato per migliorare l'accuratezza della stima dello stato nei sistemi dinamici. Appartiene alla famiglia degli algoritmi di smoothing ed estende le capacità del filtro di Kalman, che stima lo stato di un sistema in tempo reale. Mentre il filtro di Kalman elabora i dati in modo sequenziale e stima lo stato corrente basandosi esclusivamente sulle misurazioni passate e presenti, lo smoother RTS fa un ulteriore passo avanti utilizzando sia le misurazioni passate che quelle future per perfezionare le stime dello stato retrospettivamente. Questo processo si traduce in stime dello stato significativamente più accurate, soprattutto nelle applicazioni che prevedono la post-elaborazione dei dati.
Come funziona l'RTS?
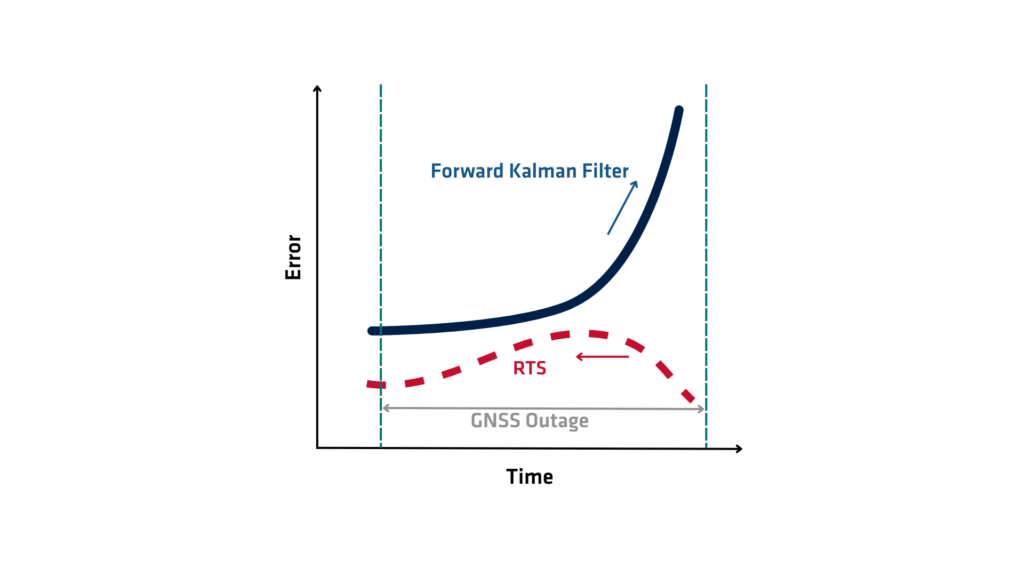
Il filtro RTS (Rauch-Tung-Striebel) o smoother RTS opera in due fasi principali: il passaggio in avanti e il passaggio all'indietro. Durante il passaggio in avanti, l'algoritmo esegue un filtro di Kalman standard attraverso i dati, raccogliendo le stime dello stato e le relative covarianze di errore a ogni passo temporale. Questa fase pone essenzialmente le basi fornendo le stime iniziali dello stato e le misure di incertezza, basate solo sui dati passati fino a ogni punto nel tempo.
Una volta completato il passaggio in avanti, inizia il passaggio all'indietro. L'algoritmo procede a ritroso dalla stima dello stato finale verso quella iniziale. A ogni passo temporale, l'RTS (Rauch-Tung-Striebel) rivede la stima dello stato incorporando informazioni provenienti dai passi temporali futuri, informazioni che non erano disponibili durante il processo di filtraggio in avanti. Utilizza il guadagno di Kalman, le matrici di transizione e le covarianze calcolate nel passaggio in avanti per calcolare una stima smoothed che bilancia sia le osservazioni passate che quelle future. Questa ricorsione all'indietro corregge le stime filtrate, riducendo l'errore di stima complessivo e producendo una traiettoria più coerente e accurata degli stati del sistema
Matematicamente, lo smoother applica una fase di correzione che sfrutta la correlazione tra gli errori nelle stime successive. Modellando l'evoluzione del sistema attraverso un processo gaussiano lineare, lo smoother RTS assume le stesse dinamiche e gli stessi modelli di misurazione utilizzati nel filtro di Kalman. Calcola un guadagno di smoothing a ogni passo, che determina la quantità di stima futura da utilizzare per regolare la stima corrente. Questo guadagno dipende dalle matrici di covarianza delle stime filtrate e dallo stato previsto.
Vantaggi di RTS (Rauch-Tung-Striebel)
Lo smoother RTS produce una stima globalmente ottimale per l'intera sequenza di stati del sistema. Presuppone che i modelli siano lineari e gaussiani. Il filtraggio stima solo lo stato corrente. Lo smoothing ricostruisce le migliori stime degli stati passati utilizzando tutti i dati disponibili. Questo rende lo smoothing particolarmente utile per le applicazioni offline.
Lo smoother RTS trova applicazione in diversi ambiti, tra cui la navigazione aerospaziale, l'elaborazione dei segnali, la finanza e la robotica. Nei sistemi di navigazione inerzialeINS), ad esempio, viene spesso utilizzato per post-elaborare i dati della traiettoria per ridurre la deriva e il rumore. Allo stesso modo, l'analisi delle serie temporali o il tracciamento degli oggetti ne fanno uso per affinare le stime in tempo reale e recuperare percorsi o tendenze precisi.
Lo smoother RTS offre dei vantaggi, ma necessita di un accesso completo al set di dati e diventa computazionalmente intensivo per dati lunghi o complessi. Inoltre, si basa molto sull'ipotesi di una dinamica lineare e di un rumore gaussiano. Quando il sistema non è lineare o il rumore non è gaussiano, si può utilizzare lo smoother RTS esteso o non accentuato. Queste varianti adattano il metodo a filtri non lineari come l'Extended Kalman Filter (EKF) o l'Unscented Kalman Filter (UKF).
Lo smoother RTS perfeziona il filtraggio di Kalman utilizzando i dati futuri per aggiornare le stime passate, migliorando la precisione e la stabilità. Costituisce la base della stima degli stati e consente una ricostruzione precisa dei sistemi dinamici utilizzando dati post-elaborati.