L'Extended Kalman Filter (EKF) è un potente strumento utilizzato nei sistemi di navigazione e controllo per stimare lo stato di un sistema che evolve nel tempo. È un'estensione del filtro di Kalman, progettato per gestire sistemi non lineari, rendendolo fondamentale per le applicazioni in cui la relazione tra le variabili non è lineare.
Questo potente algoritmo viene utilizzato per stimare lo stato di un sistema dinamico basato su misurazioni rumorose del sensore. Si basa sul filtro di Kalman standard accogliendo sistemi non lineari, che sono comuni negli scenari di navigazione del mondo reale. Mentre il filtro di Kalman tradizionale presuppone dinamiche lineari e rumore gaussiano, l'EKF supera queste limitazioni linearizzando il sistema non lineare attorno alla stima corrente. Ciò gli consente di operare efficacemente in ambienti più complessi e reali.
Principio di base del filtro di Kalman esteso
Nel suo nucleo, l'EKF aggiorna continuamente un vettore di stato, ovvero un insieme di variabili che descrivono la condizione attuale del sistema, come posizione, velocità e orientamento nei contesti di navigazione. Si basa su un modello di processo per prevedere come lo stato evolve nel tempo, incorporando la dinamica del sistema e gli input di controllo. Nel frattempo, il modello di misurazione collega i dati dei sensori in entrata allo stato stimato e una matrice di covarianza rappresenta l'incertezza sia nelle previsioni che nelle osservazioni, aiutando l'EKF a bilanciare la fiducia tra le stime del modello e gli input dei sensori.
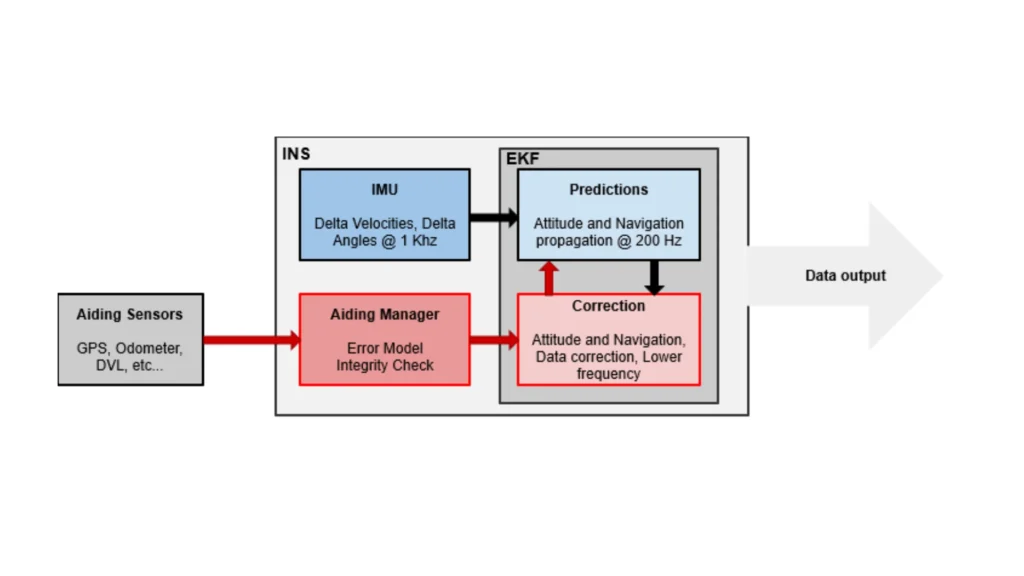
Il filtro opera in due fasi principali: previsione e aggiornamento. Durante la fase di previsione, utilizza il modello di processo per prevedere lo stato successivo e prevedere l'incertezza associata aggiornando la matrice di covarianza. Per gestire la non linearità, l'EKF linearizza sia il processo che i modelli di misurazione utilizzando le matrici Jacobiane, rappresentazioni matematiche che approssimano il comportamento del sistema vicino alla stima corrente.
Nella fase di aggiornamento, l'EKF incorpora nuove misurazioni del sensore per perfezionare la sua previsione. Calcola il guadagno di Kalman, che determina quanto peso assegnare alle nuove misurazioni rispetto allo stato previsto. Questo guadagno consente all'EKF di regolare di conseguenza la stima dello stato e aggiornare la covarianza per riflettere la ridotta incertezza dopo la misurazione.
Applicazione dell'EKF nelle applicazioni moderne
L'EKF è ampiamente utilizzato nei moderni sistemi di navigazione grazie alla sua capacità di fornire stime accurate dello stato in presenza di rumore e complessità del sistema. Ad esempio, i sistemi di navigazione inerzialeINS) si basano su accelerometri e giroscopi, che sono soggetti a deriva e rumore. L'EKF combina i dati dei sensori per fornire stime stabili di posizione, velocità e orientamento per le piattaforme dinamiche. Queste stime sono fondamentali per il funzionamento affidabile di veicoli autonomi, aerei e altri sistemi mobili.
Nella robotica e nei sistemi autonomi, l'EKF consente una localizzazione e una mappatura affidabili. I robot utilizzano sensori come LiDAR o telecamere per stimare la posizione e aggiornare le mappe utilizzando un Extended Kalman Filter (EKF). Ciò consente la mappatura e la localizzazione in tempo reale, supportando un funzionamento sicuro e autonomo in ambienti sconosciuti o dinamici.
In ambito aerospaziale e della difesa, l'EKF svolge un ruolo fondamentale nei sistemi di guida e tracciamento. Consente ad aeromobili, missili e veicoli spaziali di mantenere una posizione e una traiettoria precise, anche in condizioni di movimento non lineare. L'EKF continua a funzionare in modo affidabile quando esposto a disturbi esterni che potrebbero altrimenti degradare l'accuratezza della navigazione.
La tecnologia alla base dell'EKF include diversi componenti critici. Le matrici Jacobiane supportano il processo di linearizzazione, mentre la sensor fusion integra i dati provenienti da più fonti per garantire resilienza e accuratezza. Per supportare il funzionamento in tempo reale, l'EKF dipende da algoritmi computazionali efficienti per operazioni matriciali, aggiornamenti di covarianza e integrazione delle misurazioni.
In conclusione, il filtro di Kalman esteso (Extended Kalman Filter, EKF) è uno strumento essenziale nei sistemi di navigazione avanzati. Estendendo il filtro di Kalman per gestire i sistemi non lineari, si ottiene una stima dello stato accurata e in tempo reale. Supporta un'ampia gamma di applicazioni, tra cui la robotica, ADAS automobilistici, l'aerospazio e i sistemi di difesa. Padroneggiare i principi e le tecnologie dell'EKF è fondamentale per sviluppare soluzioni di navigazione ad alte prestazioni in ambienti complessi e dinamici.
