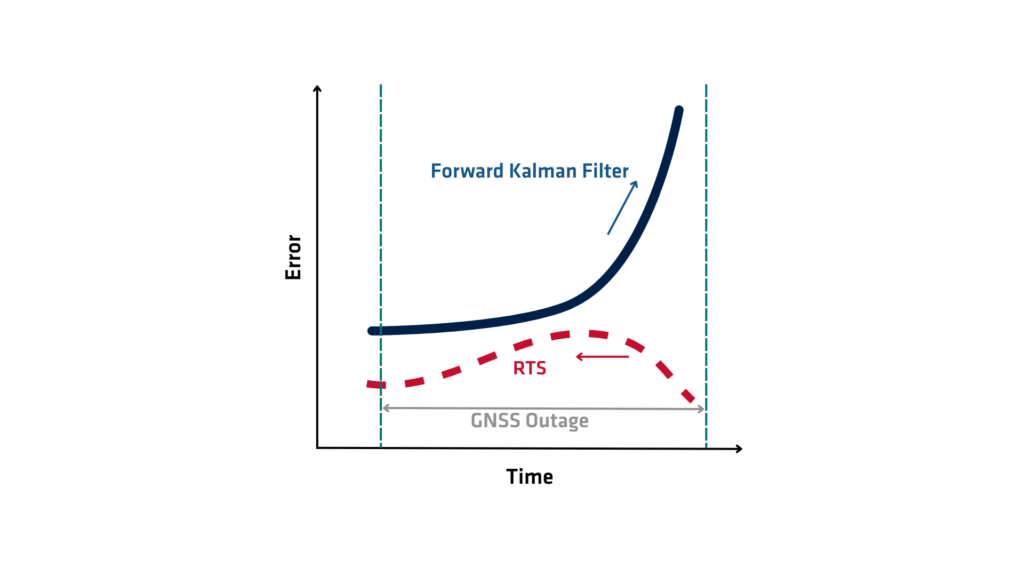
El suavizador RTS (Rauch-Tung-Striebel) es un algoritmo matemático utilizado para mejorar la precisión de la estimación del estado en sistemas dinámicos. Pertenece a la familia de los algoritmos de suavizado y amplía las capacidades del filtro de Kalman, que estima el estado de un sistema en tiempo real. Mientras que el filtro de Kalman procesa los datos secuencialmente y estima el estado actual basándose únicamente en las mediciones pasadas y presentes, el suavizador RTS va un paso más allá al utilizar tanto las mediciones pasadas como las futuras para refinar las estimaciones del estado de forma retrospectiva. Este proceso da como resultado estimaciones del estado significativamente más precisas, especialmente en aplicaciones que implican el post-procesamiento de datos.
¿Cómo funciona el RTS?
El suavizador RTS (Rauch-Tung-Striebel) opera en dos etapas principales: el paso hacia adelante y el paso hacia atrás. Durante el paso hacia adelante, el algoritmo ejecuta un filtro de Kalman estándar a través de los datos, recogiendo estimaciones del estado y las covarianzas de error asociadas en cada paso de tiempo. Esta etapa esencialmente sienta las bases proporcionando las estimaciones iniciales del estado y las medidas de incertidumbre, basándose únicamente en los datos pasados hasta cada punto en el tiempo.
Una vez que se completa el paso hacia adelante, comienza el paso hacia atrás. El algoritmo retrocede desde la estimación del estado final hacia la inicial. En cada paso de tiempo, el RTS (Rauch-Tung-Striebel) revisa la estimación del estado incorporando información de los pasos de tiempo futuros, información que no estaba disponible durante el proceso de filtrado hacia adelante. Utiliza la ganancia de Kalman, las matrices de transición y las covarianzas calculadas en el paso hacia adelante para calcular una estimación suavizada que equilibra tanto las observaciones pasadas como las futuras. Esta recursión hacia atrás corrige las estimaciones filtradas, reduciendo el error de estimación general y produciendo una trayectoria más consistente y precisa de los estados del sistema
Matemáticamente, el suavizador aplica un paso de corrección que aprovecha la correlación entre los errores en las estimaciones sucesivas. Al modelar la evolución del sistema a través de un proceso gaussiano lineal, el suavizador RTS asume la misma dinámica y los mismos modelos de medición utilizados en el filtro de Kalman. Calcula una ganancia de suavizado en cada paso, que determina la cantidad de la estimación futura que debe utilizarse para ajustar la estimación actual. Esta ganancia depende de las matrices de covarianza de las estimaciones filtradas y del estado predicho.
Ventajas de RTS (Rauch-Tung-Striebel)
El suavizador RTS produce una estimación globalmente óptima para toda la secuencia de estados del sistema. Asume que los modelos son lineales y gaussianos. El filtrado solo estima el estado actual. El suavizado reconstruye las mejores estimaciones del estado pasado utilizando todos los datos disponibles. Esto hace que el suavizado sea especialmente valioso para las aplicaciones fuera de línea.
El suavizador RTS encuentra aplicación en varios dominios, incluyendo la navegación aeroespacial, el procesamiento de señales, las finanzas y la robótica. En los sistemas de navegación inercial (INS), por ejemplo, se utiliza a menudo para el post-procesamiento de datos de trayectoria para reducir la deriva y el ruido. Del mismo modo, el análisis de series temporales o el seguimiento de objetos lo utiliza para refinar las estimaciones en tiempo real y recuperar trayectorias o tendencias precisas.
El suavizador RTS ofrece ventajas, pero necesita acceso completo al conjunto de datos y se vuelve computacionalmente intensivo para datos largos o complejos. También se basa en gran medida en la suposición de dinámica lineal y ruido gaussiano. Utilice el suavizador RTS extendido o Unscented cuando el sistema no sea lineal o el ruido no sea gaussiano. Estas variantes adaptan el método a filtros no lineales como el Filtro de Kalman Extendido (EKF) o el Filtro de Kalman Unscented (UKF).
El suavizador RTS refina el filtrado de Kalman utilizando datos futuros para actualizar las estimaciones pasadas, mejorando la precisión y la estabilidad. Forma la base de la estimación del estado y permite la reconstrucción precisa de sistemas dinámicos utilizando datos post-procesados.